Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi: 30 phút = \(\dfrac{1}{2}\) (h)
Gọi quãng đường AB là x (km) (x>0)
Vận tốc lúc đi của người đi xe máy là 30 km/h
Thì thời gian lúc đi của người đi xe máy là \(\dfrac{x}{30}\) (h)
Vận tốc lúc về của người đi xe máy là 24 km/h
Thì thời gian lúc về của người đi xe máy là \(\dfrac{x}{24}\) (h)
Theo bài ra ta có pt:
\(\dfrac{x}{24}\) - \(\dfrac{x}{30}\) = \(\dfrac{1}{2}\)
⇔\(\dfrac{5x}{120}\) - \(\dfrac{4x}{120}\) = \(\dfrac{60}{120}\)
⇔ 5x - 4x = 60
⇔ x = 60 (TM)
Vậy quãng đường AB dài 60 km.
Gọi độ dài quãng đường AB là x
Theo đề,ta có phương trình:
\(\dfrac{x}{24}-\dfrac{x}{30}=\dfrac{1}{2}\)
\(\Leftrightarrow x=\dfrac{1}{2}:\left(\dfrac{1}{24}-\dfrac{1}{30}\right)=60\)

30 phút = (1/2) giờ
Gọi quãng đường AB là x (km). Điều kiện x > 0.
Thời gian xe máy đi từ A đến B là x/30 (giờ).
Thời gian xe máy đi từ B về A là x/24 (giờ).
Ta có phương trình:
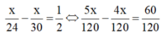
⇔ 5x - 4x = 60 ⇔ x = 60 (thỏa mãn điều kiện)
Vậy quãng đường AB là 60 km.

Gọi độ dài quãng đường AB là x (km; x > 0)
Vận tốc đi từ B trở về A là: 24 + 6 = 30 (km/h)
Thời gian người đó đi từ A đến B là:
x/24 (h)
Thời gian người đó đi từ B về A là:
x/30 (h)
Đổi 30 phút = 1/2h
vì thời gian về ít hơn thời gian đi 1/2 h nên ta có phương trình:
x/24 - x/30 = 1/2
<=> 30x/720 - 24x/720 = 360/720
<=> 30x - 24x = 360
<=> 6x = 360
<=> x = 360 : 6
<=> x = 60 (TM)
Vậy.....

Gọi độ dài quãng đường AB là x
Thời gian đi là x/40(h)
Thời gian về là x/35(h)
Theo đề, ta có: x/35-x/40=1/2
hay x=140

Gọi độ dài AB là x
Thời gian đi là x/30
Thời gian về là \(\dfrac{x+10}{25}\)
Theo đề, ta có: (x+10)/25-x/30=4/5
=>x/25-2/5-x/30=4/5
=>x/150=6/5
=>x=180
`->` gọi quãng đường `AB` là : `x(km;x>0)`
`-` quãng đường của xe máy lúc về là : `x+10(km)`
`-` thời gian của xe máy khi đi từ `A` đến `B` là : `x/30` (giờ)
`-` đổi `48` phút `=4/5` giờ
`=>` theo bài ra ta có được phương trình như sau :
`(x+10)/25-x/30=4/5`
`<=>6x -60+5x=120`
`<=>x=120-60`
`<=>x=60` (nhận)
Vậy quãng đường `AB` là `60km`

Gọi độ dài quãng đường AB là x ( km, x>0 )
Thời gian xe máy đi từ A đến B = x/30 (giờ)
Vận tốc xe máy đi từ B về A = 30+10=40km/h
Thời gian xe máy đi từ B về A là x/40 (giờ)
Theo bài ra ta có phương trình :
x/30 - x/40 = 3/4
<=> x( 1/30 - 1/40 ) = 3/4
<=> x.1/120 = 3/4
<=> x = 90 (tm)
Vậy quãng đường AB dài 90km

Gọi quãng đường AB là x (km, x>0)
Người đó đi xe đạp từ A đến B với vận tốc 15km/h
\(\to\) Thời gian lúc đi của người đó là \(\dfrac{x}{15}\) (h)
Người đó đi xe đạp từ B về A với vận tốc 12km/h
\(\to\) Thời gian lúc về của người đó là \(\dfrac{x}{12}\) (h)
Vì thời gian về nhiểu hơn thời gian đi là 30 phút
\(\to\) Ta có pt: \(\dfrac{x}{12}-\dfrac{x}{15}=\dfrac{30}{60}\)
\(\to 5x-4x=30\)
\(\to x=30\) (TM)
Vậy quãng đường AB là 30km

gọi độ dài quãng đường AB là x(km)(x>0)
độ dài quãng đường khác là x+15(km)
thời gian đi là: \(\frac{x}{30}\left(h\right)\)
thời gian về là:\(\frac{x+15}{40}\left(h\right)\)
theo đề bài: thời gian về ít hơn thời gian đi là 20 phút\(=\frac{1}{3}h\) nên ta có PT
\(\frac{x}{30}-\frac{x+15}{40}=\frac{1}{3}\)
\(\Leftrightarrow\frac{4x}{120}-\frac{3\left(x+15\right)}{120}=\frac{40}{120}\)
\(\Leftrightarrow4x-3x-45=40\)
\(\Leftrightarrow x=95\left(tmđk\right)\)
vậy đọ dài quãng đường AB là 95 km
Đổi: 20 phút = 1/3 h Gọi quãng đường AB là x (km) (x>0) Thời gian lúc đi là: x/30 (h) QĐ lúc về là: x + 15 (km) Thời gian lúc về là: (x + 15)/40 (h) Vì thời gian về ít hơn thời gian đi 20 phút nên ta có PT: x/30 - (x+15)/40 = 1/3 => ( x - 45)/120 = 1/3 => x - 45 = 40 => x = 85 (km) Vậy quãng đường AB dài 85 km

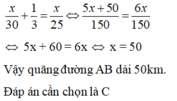
Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Theo đề, ta có phương trình:
\(\dfrac{x}{24}-\dfrac{x}{30}=\dfrac{1}{2}\)
\(\Leftrightarrow x\cdot\dfrac{1}{120}=\dfrac{1}{2}\)
hay \(x=\dfrac{1}{2}:\dfrac{1}{120}=\dfrac{1}{2}\cdot120=60\left(thỏa\right)\)
Vậy: Độ dài quãng đường AB là 60km