Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
\(s'=300m=0,3km\)
\(t'=1p=\dfrac{1}{60}h\)
\(s''=3,6km\)
\(t''=0,5h\)
a. \(v',v''=?\left(\dfrac{km}{h}\right)\)
b. \(v_{tb}=?\left(\dfrac{km}{h}\right)\)
Giải:
a. Vận tốc của người đó trên từng quãng đường:
\(\left[{}\begin{matrix}v'=s':t'=0,3:\dfrac{1}{60}=18\left(\dfrac{km}{h}\right)\\v''=s'':t''=3,6:0,5=7,2\left(\dfrac{km}{h}\right)\end{matrix}\right.\)
b. Vận tốc tb của người đó trên cả hai quãng đường:
\(v_{tb}=\dfrac{s'+s''}{t'+t''}=\dfrac{0,3+3,6}{\dfrac{1}{60}+0,5}=\dfrac{243}{31}\simeq7,55\left(\dfrac{km}{h}\right)\)

đổi 0,36 km = 360m,18 km =18000m
1 phút <=> 60 giây
Quãng đường thứ nhất đi với vận tốc là :
V1= S1/T1 = 360/60 = 6 (m/s)
Quãng đường thứ hai đi với vận tốc :
V2= S2/T2 = 18000/3600 = 5 (m/s)
Ta có :
Vtb = S1+S2/T1+T1 = 360+18000/60+3600 = 306/61 (m/s)

5 phút = 300s
a) Vận tốc trung bình của người đó trên quãng đường đầu:
\(v_1=\dfrac{s_1}{t_1}=\dfrac{300}{150}=2\left(m/s\right)\)
b) Vận tốc trung bình của người đó trên quãng đường sau:
\(v_2=\dfrac{s_2}{t_2}=\dfrac{900}{300}=3\left(m/s\right)\)
c) Vận tốc trung bình của người đó trên cả 2 đonạ đường:
\(v_{tb}=\dfrac{s_1+s_2}{t_1+t_2}=\dfrac{300+900}{150+300}=\dfrac{8}{3}\left(m/s\right)\)

a) Vận tốc TB quãng đường đầu tiên:
v1=s1/t1= 240/120=2(m/s)
Vận tốc TB quãng đường thứ hai:
v2=s2/t2=1800/1800=1(m/s)
Vì v1> v2 => Trên quãng đường thứ nhất người đó đi nhanh hơn.
b) Vận tốc TB của người đi xe đạp trên cả 2 quãng đường:
v(tb)= (s1+s2)/(t1+t2)= (240+1800)/(120+1800)=1,0625(m/s)

Thời gian người đó đi trên quãng đường thứ nhất:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{60}{20}=3\left(h\right)\)
Vận tốc trung bình của người đó:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{60+20}{3+0,5}=\dfrac{160}{7}\left(km/h\right)\)
Thời gian của người đi xe đạp trên quãng đường thứ nhất:
v1=\(\dfrac{s_1}{t_1}\)⇒t1=\(\dfrac{s_1}{v_1}\)\(\)=\(\dfrac{60}{20}\)=3(giờ)
Vận tốc trung bình của người đó trên cả hai quãng đường:
vtb=\(\dfrac{s_1+s_2}{t_1+t_2}\)=\(\dfrac{60+20}{3+0,5}\)=\(\dfrac{160}{7}\)≈22,9(km/h)

Thời gian người đó đi quãng đường đầu đó là :
\(t_1=\dfrac{s_1}{v_1}=\dfrac{3}{7,2}=0,42h.\)
Vận tốc trung bình người đó đi cả hai quãng đường là :
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{3+1,95}{0,42+0,5}=5,38\left(\dfrac{km}{h}\right)\)
Thời gian người đi bộ đi hết quang đường thứ nhất là:
v1 = s1/t1= 3000/2 = 1500 (m/s)
Thời gian người đi bộ đi hết quãng đường thứ 2 là:
t2 = 0,5 . 3600 = 1800 (m/s)
Vận tốc trung bình của người đó trên cả hai quãng đường:
vtb = (s1+s2)/(t1+t2) = (3000 + 1950)/(1500 + 1800) = 1,5 (m/s)

a. \(t''=s'':v''=1,8:\left(5.3,6\right)=0,1h\)
\(v=\dfrac{s'+s''}{t'+t''}=\dfrac{6+1,8}{0,5+0,1}=13\left(\dfrac{km}{h}\right)\)
b. \(v_{sau}=v+2=13+2=15\left(\dfrac{km}{h}\right)\)
\(20p=\dfrac{1}{3}h\)
\(s_{AB}=v_{sau}.t_{sau}=15.\dfrac{1}{3}=5km\)
+ Quãng đường đầu s 1 = 2km = 2000m;
Quãng đường sau s 2 = l,5km = 1500m;
Thời gian đi hết quãng đường sau t 2 - 0,4.3600 = 1440s.
+ Thời gian đi hết quãng đường đầu: t 1 = s 1 / v 1 = 2000/2 = 1000(s)
+ Tổng thời gian đi là: t = t 1 + t 2 = 2440 s
+ Tổng quãng đường: s = s 1 + s 2 = 2000 + 1500 = 3500m.
+ Vận tốc trung bình trên cả quãng đường là: v tb = s/t = 3500/2400 = 1,43 (m/s)
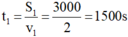
Vận tốc của người đó trên quãng đường 1 là
\(v=\dfrac{s}{t}=300:60=5\left(ms\right)\)
Vận tốc của người đó trên quãng đường 2 là
\(v=\dfrac{s}{t}=\dfrac{3,6}{0,5}=7,2\left(kmh\right)\)
Vận tốc của người đó trên cả 2 quãng đường là
\(v_{tb}=\dfrac{s'+s}{t+t'}=\dfrac{300+3600}{1800+60}=\dfrac{3900}{1860}=2,096\left(ms\right)\)
a) Vận tốc xe đi được trên quãng đường 1 là :
\(v_1=\dfrac{s_1}{t_1}=\dfrac{300}{60}-5\left(m/s\right).\)
Vận tốc xe đi được trên quãng đường 2 là :
\(v_2=\dfrac{s_2}{t_2}=\dfrac{3600}{1800}=2\left(m/s\right).\)
b) Vận tốc trung bình trên cả quãng đường là :
\(v_{tb}=\)\(\dfrac{s_1+s_2}{t_1+t_2}\)\(=\dfrac{300+3600}{60+1800}\)\(=2,1\left(m/s\right)\)