Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3h41' = \(3\frac{41}{60}\)phút.
Gọi đoạn đường bằng là x.
tổng 2 đoạn đường lên dốc và xuống dốc là 9-x, người đó phải đi đoạn đường 9-x hai lần, một lần với vận tốc 4km/h, một lần vơí vận tốc 6km/h.
Ta có PT:
\(\frac{2x}{5}+\frac{9-x}{4}\frac{9-x}{6}=3\frac{41}{60}\)
Giải PT này ta được x=4.
Vậy đoạn đường bằng dài 4km.

Gọi x (km) là độ dài quãng đường AM (x > 0)
Gọi y (km) là độ dài quãng đường BM (y > 0)
Thời gian đi từ A đến B: \(\dfrac{x}{9}+\dfrac{y}{18}=2\) (1)
Thời gian đi từ B về A: \(\dfrac{x}{18}+\dfrac{y}{9}=3\) (2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{x}{9}+\dfrac{y}{18}=2\\\dfrac{x}{18}+\dfrac{y}{9}=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=36\\x+2y=54\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+2y=72\\x+2y=54\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x=18\\2x+y=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\left(nhận\right)\\2.6+y=36\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=6\left(nhận\right)\\y=24\left(nhận\right)\end{matrix}\right.\)
Vậy AM = 6 km, MB = 24 km

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
* Lúc đi từ A đến B: Đoạn lên dốc dài 4km và đoạn xuống dốc dài 5km
* Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 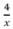 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 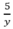 (h)
(h)
Theo đầu bài thời gian đi A đến B là 40 phút = 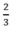 h nên:
h nên:
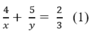
* Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 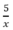 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 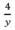 (h)
(h)
Theo đầu bài thời gian đi A đến B là 41 phút = 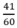 h nên:
h nên:
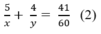
Từ (1) và (2) ta có hệ phương trình:
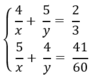
Đặt 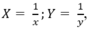 hệ phương trình trên trở thành:
hệ phương trình trên trở thành:
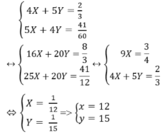
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

Gọi vận tốc lúc lên dốc và vận tốc lúc xuống dốc theo thứ tự là x, y (km/h) (x, y > 0)
* Lúc đi từ A đến B: Đoạn lên dốc dài 4km và đoạn xuống dốc dài 5km
* Lúc đi từ B đến A: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 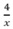 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 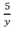 (h)
(h)
Theo đầu bài thời gian đi A đến B là 40 phút = 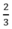 h nên:
h nên:
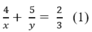
* Lúc đi từ B đến A qua C: Đoạn lên dốc dài 5 km và đoạn xuống dốc dài 4 km
Thời gian đi lên dốc là 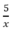 ( h) , thời gian xuống dốc là:
( h) , thời gian xuống dốc là: 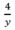 (h)
(h)
Theo đầu bài thời gian đi A đến B là 41 phút = 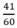 h nên:
h nên:
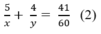
Từ (1) và (2) ta có hệ phương trình:
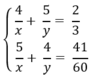
Đặt 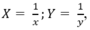 hệ phương trình trên trở thành:
hệ phương trình trên trở thành:
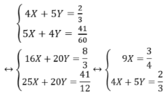
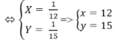
Vậy vậy tốc độ lúc lên dốc là 12km/h, vận tốc lúc xuống dốc là 15km/h.

Gọi a (km/h) là vận tốc lên dốc (theo gt vận tốc lên dốc đi và về = nhau ) (a > 0).
Gọi b (km/h) là vận tốc lên dốc (theo gt vận tốc xuống dốc đi và về = nhau ) (b > 0).
Theo đề bài ta có HPT: 4/a + 5/b = 40 5/a + 4/b = 41
Giải hệ (đặt ẩn phụ) ta được a = 1/5, b = 1/4.
Vậy vận tôc lên dốc là 1/5 km/h, xuống dốc là 1/4 km/h.

Lời giải:
Đổi $4h30'=4,5$h
Thời gian đi quãng đường $AC$: $\frac{AC}{30}$ (h)
Thời gian đi quãng đường $CB$: $\frac{CB}{20}=\frac{AC-10}{20}$ (h)
Ta có:
$\frac{AC}{30}+\frac{AC-10}{20}=4,5$$\Leftrightarrow \frac{AC}{12}=5\Rightarrow AC=60$ (km)
$CB=60-10=50$ (km)
Lời giải:
Đổi $4h30'=4,5$h
Thời gian đi quãng đường $AC$: $\frac{AC}{30}$ (h)
Thời gian đi quãng đường $CB$: $\frac{CB}{20}=\frac{AC-10}{20}$ (h)
Ta có:
$\frac{AC}{30}+\frac{AC-10}{20}=4,5$$\Leftrightarrow \frac{AC}{12}=5\Rightarrow AC=60$ (km)
$CB=60-10=50$ (km)

Gọi chiều dài đoạn lên dốc là \(x\) km
Chiều dài đoạn đường bằng là \(x+110\)
Thời gian lên dốc: \(\frac{x}{20}\) giờ
Thời gian đi đoạn đường bằng: \(\frac{x+110}{40}\)
Theo bài ra ta có pt:
\(\frac{x}{20}+\frac{x+110}{40}=\frac{7}{2}\)
\(\Leftrightarrow3x+110=140\)
\(\Rightarrow x=10\)
Vậy chiều dài cả đoạn đường là: \(10+10+110=130\) km