Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 chiếc giày trong số 8 chiếc giày.
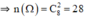
A: “ Chọn được 2 chiếc tạo thành một đôi”
⇒ n(A) = 4 (Vì có 4 đôi).
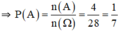
\(n\left(\Omega\right)=C^4_{10}=210\)
A: "Không chọn được hai chiếc nào tạo thành một đôi".
\(\overline{A}\): "Chọn được ít nhất hai chiếc tạo thành một đôi".
\(n\left(\overline{A}\right)=C^1_5\cdot C_8^2=140\).
\(n\left(A\right)=210-140=70\).
\(P\left(A\right)=\dfrac{70}{210}=\dfrac{1}{3}\).
ta có : \(n\left(\Omega\right)=C^6_{20}=38760\)
a) Gọi A : " chọn ra 6 chiếc gang tay mà không tạo thành đôi nào "
=> n(A) = \(\left(C^6_{10}+C^5_{10}.C^1_5+C^4_{10}.C^2_6+C^3_{10}.C^3_7+C^2_{10}.C^4_8+C^1_{10}.C^5_9+C^6_{10}\right)=13440\)
=> P(A)= 13440 / 38760 = 112/323
" Lưu ý : ta phải bân biệt gang tay trái và gang tay phải ... tự đọc rồi tìm hiểu xem tại sao lại vậy .. ko hiểu thì hỏi lại t giải thích cho :) "
b) Gọi B :" 6 chiếc lấy ra trong đó có 1 đôi "
=> n(B) = \(C^1_{10}.C^4_9+C^1_{10}.C^3_9.C^1_6+C^1_{10}.C^2_9.C^2_7+C^1_{10}.C^1_9.C^3_8+C^1_{10}.C^4_9=20160\)
=>P(A) = 20160 / 38760 =168/323
Đáp án C.
Số cách lập số có 5 chữ số có 3 và 4 đứng cạnh nhau là 2(4.4.3.2) = 192 cách.
Số cách lập số có 6 chứ số đôi một khác nhau từ A là 5.5.4.3.2=600 cách
Suy ra xác suất cần tìm là 192 600 = 8 25
Chọn C
Ta có 
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà 
hoặc 
Vì 
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
Vậy xác suất cần tìm là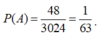 
Phép thử T được xét là: "Lấy ngẫu nhiên 2 chiếc giày từ 4 đôi giày có cỡ khác nhau".
Mỗi một kết quả có thể là một tổ hợp chập 2 của 8 chiếc giày. Do đó số các kết quả có thể có thể có của phép thử T là n(Ω) = C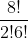28 =
= 28.
Vì lấy ngẫu nhiên, nên các kết quả có thể có của phép thử T là đồng khả năng. Gọi A là biến cố: "Lấy được hai chiếc giày tạo thành một đôi". Mỗi một kết quả có thể có thuận lợi cho A là một đôi giày trong 4 đôi giày đã cho. Do đó số các kết quả có thể có thuận lợi cho A là n(A) = 4. Suy ra P(A) =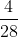
= 
.