Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng HTL trong tam giác ABC vuông tại A:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Rightarrow AB=\sqrt{\dfrac{1}{\dfrac{1}{AH^2}-\dfrac{1}{AC^2}}}=\sqrt{\dfrac{1}{\dfrac{1}{20^2}-\dfrac{1}{35^2}}}\approx24\left(m\right)\)
\(BC^2=AB^2+AC^2\left(Pytago\right)\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{24^2+35^2}\approx43\left(m\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.20.43\approx426\left(m^2\right)\)

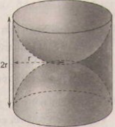
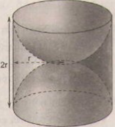
Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
Sxq = 2πrh = 2πr.2r = 4πr2
Diện tích mặt cầu:
S = 4πr2
Diện tích cần tính là:
4πr2 + 4πr2 = 8πr2

Diện tích phần cần tính gồm diện tích xung quanh của một hình trụ bán kính đường tròn đáy r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r (cm).
Diện tích xung quanh của hình trụ:
S xq = 2 π rh = 2 π r ⋅ 2 r = 4 π r 2
Diện tích mặt cầu:
S = 4 π r 2
Diện tích cần tính là:
4 π r 2 + 4 π r 2 = 8 π r 2

Diện tích phần cần tính gồm diện tích xung quanh hình trụ bán kính đường tròn đáy là r (cm), chiều cao là 2r (cm) và một mặt cầu bán kính r(cm).
Diện tích xung quanh của hình trụ:
\(S_{xq}=2\pi rh=2\pi r.2r=4\pi r^2\)
Diện tích mặt cầu:
\(S=4\pi r^2\)
Diện tích cần tính là:
\(4\pi r^2+4\pi r^2=8\pi r^2\)
DD/s >......

a:
Gọi O là trung điểm của CI
Xét tứ giác CKIH có
\(\widehat{CKI}+\widehat{CHI}=90^0+90^0=180^0\)
=>CKIH là tứ giác nội tiếp đường tròn đường kính CI
=>C,K,H,I cùng thuộc (O)
b: Xét (O) có
OI là bán kính
AB\(\perp\)OI tại I
Do đó; AB là tiếp tuyến của (O)
c: Ta có: ΔOKI cân tại O
mà OE là đường cao
nên OE là phân giác của góc KOI
Xét ΔOKE và ΔOIE có
OK=OI
\(\widehat{KOE}=\widehat{IOE}\)
OE chung
Do đó: ΔOKE=ΔOIE
=>\(\widehat{OKE}=\widehat{OIE}\)
=>\(\widehat{OKE}=90^0\)
=>EK là tiếp tuyến của (O)