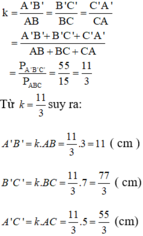Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=48/2=24dm
AB=AC=căn AH^2+HC^2=26(dm)
Xét ΔAHB có BM/BA=BE/BH=1/2
nên ME//AH và ME=1/2AH=5dm
Xét ΔCAH có CN/CA=CF/CH
nên NF//AH
=>NF/AH=CF/CH=1/2
=>NF=5dm
ΔAHB vuông tại H có HM là trung tuyến
nên HM=AB/2=13dm

\(7,\)
\(a,\left\{{}\begin{matrix}AB=AC\left(\Delta ABC.cân\right)\\\widehat{B_1}=\widehat{C_1}\left(\dfrac{1}{2}\widehat{ABC}=\dfrac{1}{2}\widehat{ACB}\right)\\\widehat{BAC}.chung\end{matrix}\right.\Rightarrow\Delta AFC=\Delta AEB\left(g.c.g\right)\\ \Rightarrow AF=AE\Rightarrow\Delta AFE.cân.tại.A\)
\(b,\left\{{}\begin{matrix}\widehat{ABC}=\widehat{ACB}\left(\Delta ABC.cân\right)\\BC.chung\\\widehat{B_2}=\widehat{C_2}\left(\dfrac{1}{2}\widehat{ABC}=\dfrac{1}{2}\widehat{ACB}\right)\end{matrix}\right.\Rightarrow\Delta BFC=\Delta CEB\left(g.c.g\right)\)
\(c,\widehat{F_1}=\dfrac{180^0-\widehat{BAC}}{2}\left(\Delta AEF.cân\right);\widehat{ABC}=\dfrac{180^0-\widehat{BAC}}{2}\left(\Delta ABC.cân\right)\\ \Rightarrow\widehat{F_1}=\widehat{ABC}\)
Mà 2 góc này ở vị trí đồng vị nên \(EF//BC\Rightarrow BEFC\) là hình thang
Mà \(\widehat{ABC}=\widehat{ACB}\left(GT\right)\)
Vậy \(BEFC\) là hình thang cân

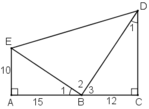
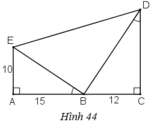
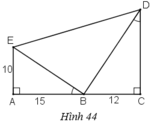
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
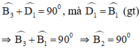
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
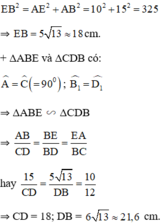
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
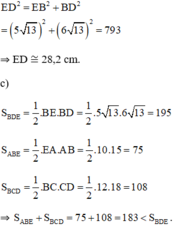

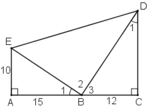
a) + ΔABE vuông tại A.
+ ΔBCD vuông tại C.
+ Ta có:
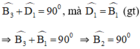
Vậy ΔBED vuông tại B.
b) + Áp dụng định lý Pytago trong ΔABE vuông tại A ta có:
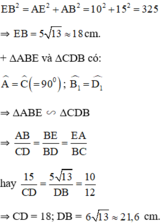
+ Áp dụng định lý Pytago trong ΔEBD vuông tại B ta có:
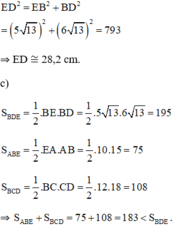

Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’ 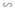 ΔABC ⇒
ΔABC ⇒ 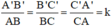
Áp dụng tính chất dãy tỉ số bằng nhau ta có: