
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


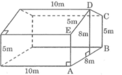
Diện tích nhà kính gồm bốn hình chữ nhật có kích thước là 5m và 10m và hai hình bằng diện tích hình ABCDE.
Diện tích bốn hình chữ nhật là: (5.10).4 =200( m 2 )
Tống diện tích kính cần dùng là: 200 + 52.2 = 304 ( m 2 )

ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
=>HB=HC=48/2=24dm
AB=AC=căn AH^2+HC^2=26(dm)
Xét ΔAHB có BM/BA=BE/BH=1/2
nên ME//AH và ME=1/2AH=5dm
Xét ΔCAH có CN/CA=CF/CH
nên NF//AH
=>NF/AH=CF/CH=1/2
=>NF=5dm
ΔAHB vuông tại H có HM là trung tuyến
nên HM=AB/2=13dm

tổng số phần bằng nhau là:
2+1=3(phần)
nhà cô Mai có số con gà trống là:
48:3x1=16(con)
nhà cô Mai có số con gà mái là:
48-16=32(con)
nhà cô mai có số con gà trống là:
48:(2+1)=16(con)
số con gà mái là
16x2=32(con)

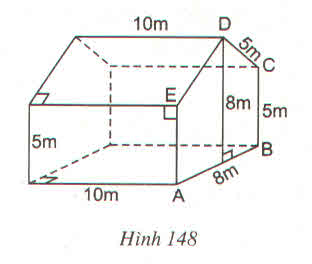
a: \(S_{ABCDE}=\dfrac{2\left(5+8\right)}{2}\cdot4=52\left(m^2\right)\)
b: \(V=S\cdot h=52\cdot10=520\left(m^{^3}\right)\)
c: Diện tích bốn hình chữ nhật là \(5\cdot10\cdot4=200\left(m^2\right)\)
Tổng diện tích cần dùng là:
200+52x2=304(m2)

a: Xét ΔABC có DE//BC
nên AN/AB=AM/AC
=>1,5/AB=2,4/5,3
=>\(AB\simeq3,3125\left(m\right)\)
b: 
Xét ΔABC có DE//BC
nên DE/BC=AE/AC=(AC-CE)/AC
=>36-x=1,6*36/24=2.4
=>x=33,6(m)
a) Xét tam giác \(ABC\) có \(MN//BC\) nên theo định lí Thales ta có:
\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} \Leftrightarrow \frac{{1,5}}{{AB}} = \frac{{2,4}}{{2,4 + 2,9}} \Rightarrow AB = \frac{{1,5.\left( {2,4 + 2,9} \right)}}{{2,4}} = 3,3125\)
Vậy chiều cao \(AB\)của cái cây là 3,3125m.
b) Đặt tên các điểm như hình vẽ

Xét tam giác \(ABC\) có \(DE//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AC - CE}}{{AC}} \Leftrightarrow \frac{{1,6}}{{24}} = \frac{{36 - x}}{{36}}\)
\( \Rightarrow 36 - x = \frac{{1,6.36}}{{24}} \Leftrightarrow x = 36 - \frac{{1,6.36}}{{24}} = 33,6\)
Vậy người đó có thể đứng xa tòa nhà nhất là 33,6m.
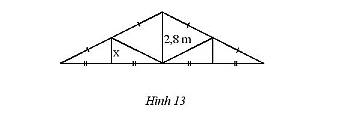


Theo hình vẽ ta có:
\(BE = EA \Rightarrow E\) là trung điểm của \(AB\);
\(BF = FH \Rightarrow F\) là trung điểm của \(BH\).
Vì \(E\)là trung điểm của \(AB\); \(F\)là trung điểm của \(BH\) nên \(EF\) là đường trung bình của tam giác \(ABH\).
\( \Rightarrow EF = \frac{1}{2}AH\) (tính chất đường trung bình)
\( \Leftrightarrow EF = \frac{1}{2}.2,8 = 1,4\).
Vậy \(x = 1,4m\).
x=2,8/2=1,4(m)