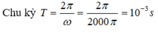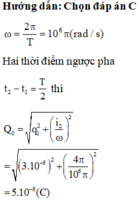K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
13 tháng 12 2016
Bài này khá quen thuộc rồi. Giải như sau:
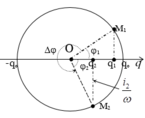
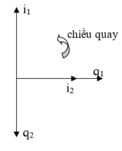
Đặt $q_1=Q_0\cos(\omega t_1)\Rightarrow i_1=Q_0\omega\cos(\omega t_1+\frac{\pi}{2})$
Sau $\frac{3T}{4}$: $i_2=Q_0\omega\cos\left ( \omega(t_1+\frac{3T}{4})+\frac{\pi}{2} \right )=Q_0\omega\cos (\omega t_1)$. $(1)$ Mà $i_1=-Q_0\omega\sin (\omega t_1)$
$\Rightarrow i_1^2+i_2^2=I_0^2$ $(\star)$
Áp dụng định luật bảo toàn năng lượng: $Li_2^2+\frac{q_2^2}{C}=LI_0^2$ $(\star \star)$
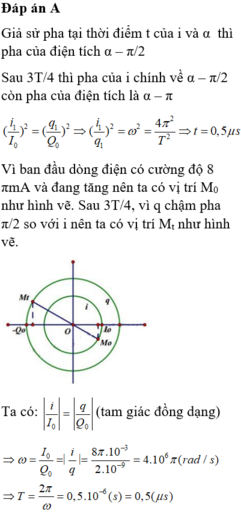
Từ $(\star), (\star \star)\Rightarrow q_2^2=LCi_1^2=\frac{i_1^2}{\omega ^2}\Rightarrow \omega=4.10^6\pi\rightarrow T=\frac{2\pi}{\omega}=5.10^7=0,5\mu s$