Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

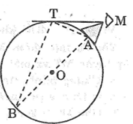
Điểm nhìn tối đa T là tiếp điểm của tiếp tuyến kẻ từ mắt đến bề mặt Trái Đất (như hình vẽ)
Xét hai tam giác MTA và MBT,ta có:
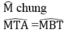
(hệ quả góc giữa tiếp tuyến và dây cung)
Suy ra ∆ MTA đồng dạng ∆ MBT
⇒ MT/MA = MB/MT => M T 2 = MA.MB
= MA (MA + 2R)
MA là chiều cao của đỉnh núi bằng 1km
Thay số ta có: M T 2 =1.(1 + 2.6400)=12801
Suy ra : MT ≈ 113,1(km)

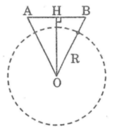
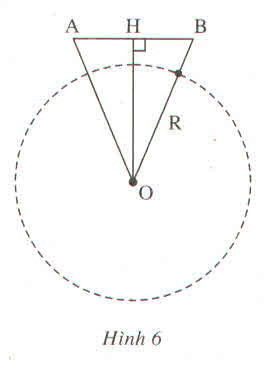
Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
Suy ra: HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
O A 2 = A H 2 + O H 2
Suy ra: O H 2 = O A 2 - A H 2
Suy ra:
OH = ![]() ≈ 6508 (km)
≈ 6508 (km)
Vì OH > R nên hai vệ tinh nhìn thấy nhau.

lAB=8050,96(km)
=>3,14*R*72/180=8050,96
=>R=6410(m)
=>OA=6410(m)
AC=6410-6400=10(m)

Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
\(\Rightarrow\): HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
OA2 = AH2 + OH2
\(\Rightarrow\): OH2 = OA2 – AH2
\(\Rightarrow\) :OH = 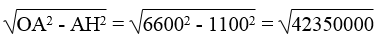
Vì OH > R nên hai vệ tinh nhìn thấy nhau.