Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Chọn 4 trong 50 bạn để quét sân, sau đó chọn 5 trong 46 bạn còn lại để xén cây. Vậy có \(C^4_{50}.C^4_{46}\) cách phân công.
Từ đó ta có đẳng thức cần chứng minh
b) Lập luận tương tự
c) Ta có : \(0!=1;2!=2;4!=1.2.3.4=24\)
Các số hạng \(6!;8!;.....,100!\) đều có tận cùng là chữ số \(0\). Do đó chữ số ở hàng đơn vị của \(S\) là \(1+2+4=7\)
Chọn ngẫu nhiên 3 bạn: \(C_{15}^3=455\) cách
Chọn 3 bạn không có mặt lớp A: \(C_{11}^3=165\) cách
Chọn 3 bạn ko có mặt lớp B: \(C_{10}^3=120\)
Chọn 3 bạn ko có mặt lớp C: \(C_9^3=84\)
a.
Chọn 3 bạn có mặt đủ 3 lớp: \(455-\left(165+120+84\right)=86\) cách
b.
Chọn 3 bạn có ít nhất 1 bạn lớp A: \(455-165=290\) cách
c.
Không hiểu ý câu hỏi?
Chọn A
Mỗi cách chọn ra 3 học sinh từ 40 học sinh để làm tổ trưởng tổ 1, tổ 2, tổ 3 là một chỉnh hợp chập 3 của 40 phần tử, vậy có: A 40 3 (cách).
Chọn C
CÁCH 1
Xét phép thử “Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác trong lớp”
Khi đó: 
Gọi A là biến cố: “4 học sinh được chọn có cả nam và nữ”.
Ta xét các trường hợp:
TH1: Chọn được 1 nữ, 3 nam. Số cách chọn là: 
TH2: Chọn được 2 nữ, 2 nam. Số cách chọn là: 
.
TH3: Chọn được 3 nữ, 1 nam. Số cách chọn là: 
.
Suy ra 
Vậy xác suất cần tìm là: 
CÁCH 2
Xét phép thử “Bạn lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác trong lớp”
Khi đó: 
Gọi A là biến cố: “4 học sinh được chọn có cả nam và nữ” thì A ¯ là biến cố: “cả 4 học sinh được chọn chỉ có nam hoặc nữ”.
Ta có 
Do đó xác suất xảy ra của biến cố
A
¯
là: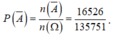 
Suy ra 
Chọn C
Gọi A: “4 học sinh được chọn có cả nam và nữ.”
=> A ¯ : “4 học sinh được chọn chỉ có nam hoặc chỉ có nữ.”
Số cách để lớp trưởng nữ chọn ngẫu nhiên 4 học sinh khác: Ω = C 44 4
Số cách chọn 4 học sinh toàn là nam: C 25 4
Số cách chọn 4 học sinh toàn là nữ: C 19 4
Xác suất để 4 học sinh được chọn có cả nam và nữ:
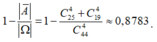
a. Chọn bất kì 5 học sinh từ 50 học sinh có: \(C_{50}^5\) cách
b. Lớp có 20 học sinh nam. Chọn 5 bạn trong đó có 2 bạn nam (suy ra 3 bạn nữ) đồng nghĩa: chọn 2 nam từ 20 nam và 3 nữ từ 30 nữ
\(\Rightarrow\) Có \(C_{20}^2.C_{30}^3\) cách
c. Số cách chọn 5 bạn toàn là nữ: \(C_{30}^5\) cách
Số cách chọn 5 bạn có ít nhất 1 nam: \(C_{50}^5-C_{30}^5\) cách
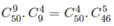
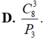
a) Cách thứ nhất: Chọn 9 bạn nam trong 50 bạn để làm trực nhật. Có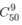
cách.
Khi đã chọnđược 9 bạn rồi, chọn 4 trong 9 bạn đó để quét sân. Có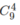
cách.
Từ đó, theo quy tắc nhân, có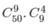
cách phân công.
Cách thứ hai: Chọn 4 trong 50 bạn để quét sân, sau đó chọn 5 trong 46 bạn còn lại để xén cây. Vậy có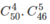
cách phân công.
Từ đó ta có đẳng thức cần chứng minh.