Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình hướng dẫn thế này rồi bạn làm tiếp nhé.
a. Áp dụng CT: \(hf=A_t+\dfrac{1}{2}mv^2\)
\(\Rightarrow 6,625.10^{-34}.3.10^8=A_t+\dfrac{1}{2}.9,1.10^{-31}.(0,4.10^6)^2\)
\(\Rightarrow A_t\)
Mà \(A_t=\dfrac{hc}{\lambda_0}\Rightarrow \lambda_0\)
b. Áp dụng: \(\dfrac{hc}{\lambda}=A_t+eV_{max}\)
\(\Rightarrow \lambda\)

Hệ thức Anh -xtanh trong hiện tượng quang điện ngoài
\(\frac{hc}{\lambda} = A+W_{đmax}\)
mà \(\lambda = \lambda_0/2\) => \(\frac{2hc}{\lambda_0} = A+W_{đmax}\)
Lại có \(A = \frac{hc}{\lambda_0}\) => \(W_{đmax}= \frac{2hc}{\lambda_0} -A= 2A - A = A.\)

Hệ thức Anh -xtanh: \(hf = A+ W_{đ max}= A+eU_h\)
Chiếu bức xạ 1:
\(A = hf_1 - \frac{1}{2}m_e.v_{0max}^2= \frac{6,625.10^{-34}.3.10^8}{0,2.10^{-6}}-\frac{1}{2}9,1.10^{-31}.(0,7.10^6)^2= 7,708.10^{-19}J\)
Chiếu bức xạ 2: \(V_{max}= U_h\)
\(hf_2 = A+eU_h= 7,708.10^{-19}+3.1,6.10^{-19}= 1,25.10^{-18}J\)
=> \(\lambda_2 = \frac{hc}{1,25.10^{-18}}= \frac{6,625.10^{-34}.3.10^8}{1,25.10^{-18}}=1,6.10^{-7}m = 0,16 \mu m.\)

Công thức Anh-xtanh:
Tấm A: \(hf = A_1+ \frac{1}{2} mv_{max1}^2\)
Tấm B: \(hf = A_2+ \frac{1}{2} mv_{max2}^2\)
=> \( A_2+ \frac{1}{2} mv_{max2}^2= A_1+ \frac{1}{2} mv_{max1}^2\)
=> \( A_2-A_1= \frac{1}{2} mv_{max1}^2- \frac{1}{2} mv_{max2}^2\)
=> \( hc (\frac{1}{\lambda_{01}}- \frac{1}{\lambda_{02}})= \frac{1}{2} mv_1^2- \frac{1}{2} mv_2^2\)
Mà: \(\lambda_{02} = 0,8\lambda_{01} \) (vì \(W_{đmax1} > W_{đmax2} => A_1 < A_2 => \lambda_{01} > \lambda_{02}\))
=> \( hc (\frac{5}{4\lambda_{01}}- \frac{1}{\lambda_{01}})= \frac{1}{2} m(v_1^2-v_2^2)\)
=> \( hc \frac{1}{4\lambda_{01}}= \frac{1}{2} m(v_1^2-v_2^2)\)
=> \(\lambda_{01} = \frac{.hc}{4.0,5.m_e.(v_1^2-v_2^2)} = \frac{6,625.10^{-34}.3.10^8}{4.0,5.9,1.10^{-31}.(5,8^2.10^{10}-4,2^2.10^{10})} = 0,683.10^{-6}m.\)
Chọn đáp án.B.0,683.10-6m.
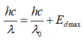
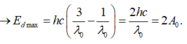



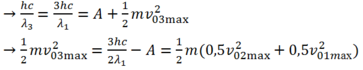

Chọn C