Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Tổng cả 4 tấm thẻ là 1 số lẻ khi
+) Có 1 thẻ là lẻ, 3 thẻ còn lại là chẵn, suy ra có C 6 1 C 5 3 = 60 cách chọn.
+) Có 3 thẻ là lẻ, 1 thẻ là chẵn, suy ra có C 5 1 C 6 3 = 100 cách chọn.
Suy ra
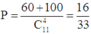

Số phần tử của không gian mẫu:
n Ω = C 11 6 = 462
Gọi A:”tổng số ghi trên 6 tấm thẻ ấy là một số lẻ”.
Từ 1 đến 11 có 6 số lẻ và 5 số chẵn.Để có tổng là một số lẻ ta có 3 trường hợp.
Trường hợp 1: Chọn được 1 thẻ mang số lẻ và 5 thẻ mang số chẵn có: 6 . C 5 5 = 6 cách.
Trường hợp 2: Chọn được 3 thẻ mang số lẻ và 3 thẻ mang số chẵn có: C 6 3 . C 5 3 = 200 cách.
Trường hợp 2: Chọn được 5 thẻ mang số lẻ và 1 thẻ mang số chẵn có: C 6 5 . 5 = 30 cách.
Do đó n(A)= 6+200+30=236.
Vậy P A = 236 462 = 118 231
Chọn đáp án D.

Số phần tử của không gian mẫu là ![]() .
.
Gọi A:”tổng số ghi trên 6 tấm thẻ ấy là một số lẻ”.
Từ 1 đến 11 có 6 số lẻ và 5 số chẵn.Để có tổng là một số lẻ ta có 3 trường hợp.
Trường hợp 1: Chọn được 1 thẻ mang số lẻ và 5 thẻ mang số chẵn có:![]() cách.
cách.
Trường hợp 2: Chọn được 3 thẻ mang số lẻ và 3 thẻ mang số chẵn có: ![]() cách.
cách.
Trường hợp 2: Chọn được 5 thẻ mang số lẻ và 1 thẻ mang số chẵn có: ![]() cách.
cách.
Do đó n(A)=6+200+30=236
Vậy 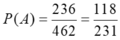 .
.
Chọn D.

Không gian mẫu: \(C_{15}^5\)
Tổng số 5 tấm thẻ là lẻ khi số số thẻ lẻ là 1 số lẻ, gồm các trường hợp: (1 thẻ lẻ, 4 thẻ chẵn), (3 thẻ lẻ, 2 thẻ chẵn), (5 thẻ đều lẻ)
Trong 15 tấm thẻ có 7 thẻ chẵn và 8 thẻ lẻ
\(\Rightarrow\) Số biến cố thuận lợi: \(C_8^1.C_7^4+C_8^3.C_7^2+C_8^5\)
Xác suất: ...



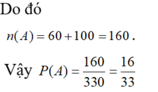


Không gian mẫu \(C_9^4\)
Các tấm bìa gồm 5 tấm số lẻ và 4 tấm số chẵn
Để tổng 4 số là số lẻ khi số số lẻ là lẻ
\(\Rightarrow\) có 1 hoặc 3 tấm bìa mang số lẻ
Số biến cố thỏa mãn: \(C_5^1C_4^3+C_5^2C_4^2\)
Xác suất: \(P=\dfrac{C_5^1C_4^3+C_5^2C_4^2}{C_9^4}\)