Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Thể tích của khối nón là V n = 1 3 π r 2 h 1 và độ dài đường sinh là l = r 2 + h 2
Thể tích của khối trụ là V t = π r 2 h 2 = 1 3 π r 2 h
Vậy thể tích cái nắp là V = V n + V t = 2 3 π r 2 h
Mặt khác l =1,25
⇒ r 2 + h 2 = 25 4 ⇔ r 2 = 25 4 − h 2
khi đó:
V = 2 3 π h 25 4 − h 2 ≤ 2 π 3 . 125 12 3
Ta có:
V 2 = 4 9 π 2 h 2 25 4 − h 2 2 ≤ 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 2 9 π 2 . 25 4 − h 2 . 25 4 − h 2 ≤ 2 π 2 9 . 25 4 + 25 4 3 3
Dấu bằng xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3
Dấu “=” xảy ra khi:
2 h 2 = 25 4 − h 2 ⇔ h 2 = 25 12 ⇒ h = 5 2 3 ⇒ r = 25 4 − h 2 = 5 6 6 ⇒ r + h ≃ 348 c m

Đáp án A
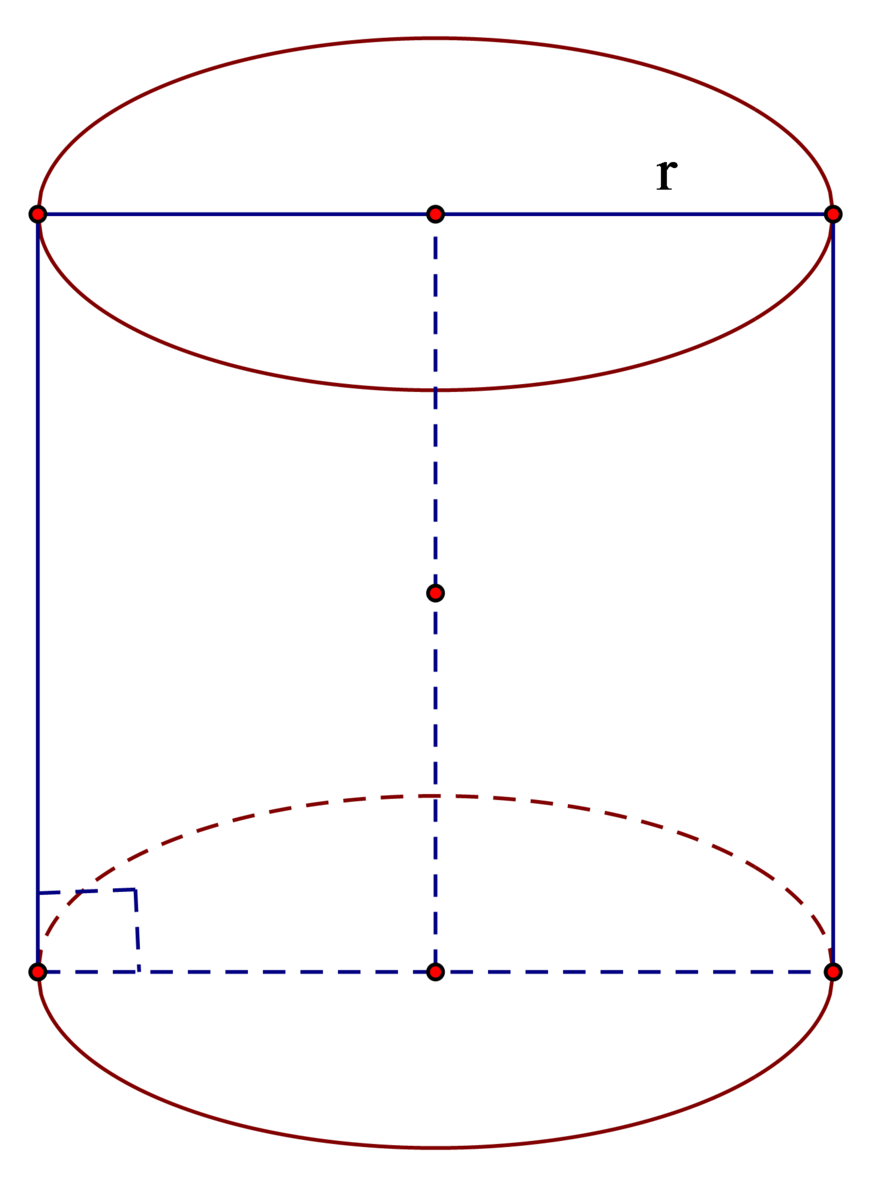
Chu vi hình tròn đáy: C = 2 π r
Thiết diện qua đáy là hình vuông nên chiều cao của hình trụ là 2 r
Vậy diện tích toàn phần của hình trụ là:
S = S x q + S d = 2 π r .2 r + 2 π r 2 = 6 π r 2

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
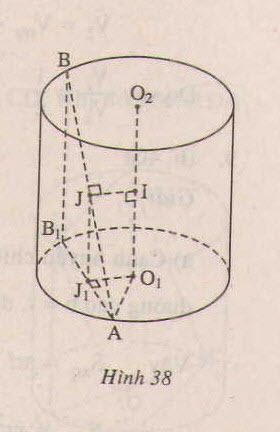
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :

Đáp án B
Phương pháp giải: Chuẩn hóa thể tích, đưa diện tích toàn phần về hàm số, khảo sát hàm (hoặc bất đẳng thức) tìm min
Lời giải:
Thể tích của khối trụ là 
Chuẩn hóa 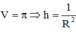
Diện tích toàn phần của hình trụ là ![]()
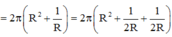
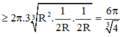
Dấu bằng xảy ra khi và chỉ khi ![]()

Đáp án D
Ta có V t = V = l . π R 2 ⇒ l = V π R 2
S t = l .2 π R + 2 π R 2 ⇒ S t = V π R 2 π R + 2 π R 2 = 2 ( π R 2 + V R )
S t = 2 ( π R 2 + V 2 R + V 2 R ) ≥ 2.3 π R 2 . V 2 R . V 2 R 3 = 6 π V 2 4 3
Dấu “=” xảy ra khi và chỉ khi π R 2 = V 2 R ⇔ R = V 2 π 3

Chọn B.
Phương pháp: Coi đáy của hình trụ là mặt phẳng cắt mặt cầu. Áp dụng công thức

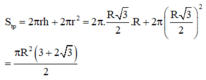

Đáp án B
Gọi h, r lần lượt là chiều cao và bán kính đường tròn đáy của hình trụ.
Khi đó, bán kính mặt cầu ngoại tiếp hình trụ là R 2 = r 2 + h 2 4
Theo bài ra, ta có h = R nên suy ra R 2 = r 2 + h 2 4 ⇔ r 2 = 3 R 2 4 ⇔ r = R 3 2
Diện tích toàn phần hình trụ là:
S t p = 2 πr 2 + 2 πrh = 2 πr r + h = 2 π . R 3 2 . R 3 2 + R = 3 + 2 3 πR 2 2 .

Đáp án B.
Ta có: V = π R 2 h ⇒ h = V π R 2 (1)
S x q = 2 π R h = 2 π . R . V π R 2 = 2 V R ; S t p = S x q + 2 S đ = 2 V R + 2 π R 2
Xét hàm số f R = 2 V R + 2 π R 2 (V là hằng số)
f ' R = − 2 V R 2 + 4 π R = 0 ⇔ R = V 2 π 3
Bảng biến thiên:
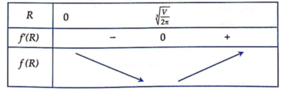
⇒ S t p min = f R min ⇔ R = V 2 π 3 ⇒ v = 2 π R 3
Từ (1)
⇒ h = V π R 2 = 2 π R 3 π R 2 = 2 R ⇒ h R = 2
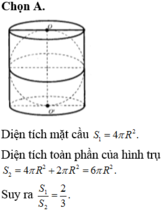
Đáp án là A