Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều dài, chiều rộng lần lượt là a,b
Theo đề, ta có hệ phương trình:
a+b=340/2=170 và 3a-4b=20
=>3a+3b=510 và 3a-4b=20
=>7b=490 và a+b=170
=>b=70 và a=100

Gọi \(x,y\left(m\right)\) lần lượt là chiều dài và rộng \(\left(x,y>0\right)\)
Theo đề, ta có :
\(\left\{{}\begin{matrix}x-20=y\\2\left(2x+3y\right)=480\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=20\\2x+3y=240\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=60\left(n\right)\\y=40\left(n\right)\end{matrix}\right.\)
Vậy chiều dài là \(60m\), chiều rộng là \(40m\)

Gọi chiều rộng là x
Chiều dài là x+20
Theo đề, ta có: 2(2x+40+3x)=480
=>5x+40=240
=>x=40
Vậy: Chiều rộng là 40m
Chiều dài là 60m

Lời giải:
Gọi chiều dài là $a$ và chiều rộng là $b$ (m)
Theo bài ra ta có:
\(\left\{\begin{matrix} a+b=340:2=170\\ 3a-4b=20\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=100\\ b=70\end{matrix}\right.\) (m)

Gọi x, y (m) lần lượt là chiều rộng và chiều dài của sân trường.
Điều kiện: 0 < x < 170; 0 < y < 170.
Vì chu vi của sân trường bằng 340 m nên ta có: 2(x + y) = 340
Vì ba lần chiều dài hơn bốn lần chiều rộng là 20m nên ta có: 3y – 4x = 20
Ta có hệ phương trình:
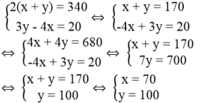
Giá trị của x và y thỏa điều kiện bài toán.
Vậy chiều rộng của sân trường là 70m,
chiều dài của sân trường là 100m.

Câu 1:
Gọi x là chiều dài mảnh đất (0<x<14; x>y)
Gọi y là chiều rộng mảnh vườn (0<y<14)
Vì chu vi mảnh đất bằng 20m nên ta có PT: x+y=14 (1)
Vì đường chéo mảnh đất bằng 10m nên ta có PT:
x2+y2=100 (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}x+y=14\\x^2+y^2=100\end{matrix}\right.\)(HPT dễ rồi bạn tự giải nha)
⇔\(\left\{{}\begin{matrix}y=8\\y=6\end{matrix}\right.\)(TM)
Vậy ta có 2 tập nghiệm (x;y) là (6;8) và (8;6)
-Độ dài 2 cạnh mảnh đất lần lượt là: 6cm và 8cm
Câu 1:
Gọi a(m) và b(m) lần lượt là chiều dài và chiều rộng của mảnh đất(Điều kiện: a>0; b>0 và \(a\ge b\))
Vì chu vi mảnh đất là 28m nên ta có phương trình:
2(a+b)=28
hay a+b=14(1)
Vì đường chéo hình chữ nhật là 10m nên Áp dụng định lí Pytago, ta được:
\(a^2+b^2=100\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}a+b=14\\a^2+b^2=100\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\\left(14-b\right)^2+b^2=100\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\b^2-28b+196+b^2-100=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\2b^2-28b+96=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\b^2-14b+48=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=14-b\\\left(b-6\right)\left(b-8\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}a=14-8=6\\b=14-6=8\end{matrix}\right.\\\left[{}\begin{matrix}b=6\\b=8\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=8\\b=6\end{matrix}\right.\)(thỏa ĐK)
Vậy: Độ dài hai cạnh của mảnh đất hình chữ nhật lần lượt là 8m và 6m


Nửa chu vi hình chữ nhật là:
140:2=70(m)
Chiều dãi hình chữ nhật là:
(70+10):2=40(m)
Chiều rộng hình chữ nhật là:
70-40=30(m)
Diện tích hình chữ nhật là:
40x30=1200(m2)
Đáp sô:1200 m2
Gọi chiều dài là x
Chiều rộng là 70-x
Theo đề, ta có:
\(3\left(70-x\right)-x=10\)
\(\Leftrightarrow210-3x-x=10\)
hay x=50
Vậy: Chiều dài là 50m
Chiều rộng là 20m