Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Thể tích hình chóp = $\frac{1}{3}$ x diện tích đáy x chiều cao.
Do đó diện tích đáy là:
$126.3:6=63$ (cm2)

Tam giác đều cạnh a có diện tích bằng a 2 3 / 4 . Do đó, hình chóp tam giác đều với cạnh đáy a, chiều cao h có thể tích :
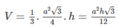
Nếu gấp đôi cả chiều cao và cạnh đáy thì thể tích hình chóp là:
![]()

Tam giác đều cạnh a có diện tích bằng \(\dfrac{a^2\sqrt{3}}{4}\) . Do đó , hình chóp tam giác đều với cạnh đáy a , chiều cao h có thể tích :
\(V=\dfrac{1}{3}.\dfrac{a^2\sqrt{3}}{4}.h=\dfrac{a^2h\sqrt{3}}{12}\)
a) Nếu tăng gấp đôi chiều cao thì thể tích hình chóp là
\(V'=\dfrac{1}{3}.\dfrac{a^2\sqrt{3}}{4}.2h=2.\dfrac{a^2h\sqrt{3}}{12}=2V\)
b) Nếu tăng gấp đôi cạnh đáy thì thể tích hình chóp là
\(V'=\dfrac{1}{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}.h=4.\dfrac{a^2h\sqrt{3}}{12}=4V\)
c) Nếu gấp đôi cả chiều cao và cạnh đáy thì thể tích hình chóp là
\(V'=\dfrac{1}{3}.\dfrac{\left(2a\right)^2\sqrt{3}}{4}.2h=8.\dfrac{a^2h\sqrt{3}}{12}=8V\)

Gọi đường cao và cạnh đáy tương ứng ban đầu là h và a
Đường cao và cạnh đáy tương ứng lúc sau là 3h và 3a
Diện tích ban đầu : \(ah\)
Diện tích lúc sau : \(\left(3a\right)\left(3h\right)=9ah\)
\(\frac{9ah}{ah}=9\), suy ra đáp số là 9
Vậy ...


9 lần nhé bạn
bạn có thể giải chi tiết hộ mik đc ko