Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
Đáp án D.
Vì hai hạt sinh ra có cùng vectơ vận tốc nên theo ĐL bảo toàn động lượng ta có;
mava = (mH + mO).v (với v là vận tốc của hai hạt sau phản ứng)
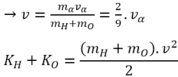
DE = KH + KO - Ka = 2/9 Ka - Ka = -7Ka/9
→ Ka = -9DE/7 = 1,5557 MeV = 1,56 MeV.
\(_1^1p + _3^7 Li \rightarrow 2_2^4He\) => X là Heli.
Áp dụng định luật bảo toàn động lượng trước và sau phản ứng
\(\overrightarrow P_{p} = \overrightarrow P_{He_1} + \overrightarrow P_{He_2}\) , do \( (\overrightarrow P_{Li} = \overrightarrow 0)\)
Dựa vào hình vẽ ta có
\(P_p^2 + P_{He_1}^2 - 2P_pP_{He_1} \cos {60^o}= P_{He_2}^2\)
Mà \(P_{He_1} = P_{He_2}\)
=> \(P_p^2 - 2P_pP_{He} \cos {60^o}= 0\)
=> \(P_p^2 =2P_pP_{He} \cos {60^o}\)
=> \(P_p =P_{He} \)
=> \(m_pv_p=m_{He}v_{He} \)
=> \(\frac{v_p}{v_{He}} = 4.\)
Đáp án A
Ta có: 
+ Thay vào phương trình mO.ma = 0,21(mO + mp)2 ® ma = 4,107mp
+ Vì 2 hạt sinh ra có cùng vận tốc nên: Ka.ma = (mO + mp).(Ka - 1,21)
→ Ka = 1,555 MeV.
Ta có phương trình phản ứng là:
Sau phản ứng tạo thành 2 hạt He, bay theo hai hướng tạo với hướng của p ban đầu một góc 800.
Áp dụng định luật bảo toàn động lượng, ta có hình biểu diễn các vecto động lượng
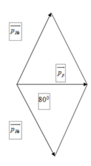
Áp dụng định lý sin trong tam giác ta có:
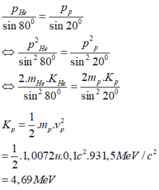
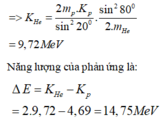
Đáp án B
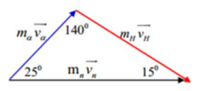
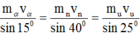
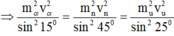
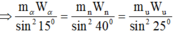
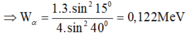
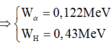
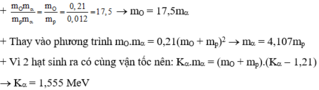
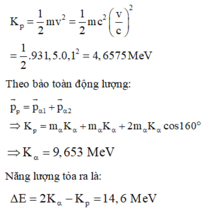
Đáp án: B.
Ta có phương trình phản ứng: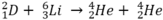
Theo ĐL bảo toàn động lượng: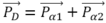
và P2 = 2mK (K là động năng)
PD2 = Pα12 + Pα22 + 2Pα1Pα2cos(157o)
Mặt khác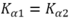
, giải (1) ta được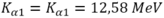 
Năng lượng phản ứng: ∆ E = Kα1 + Kα2 – KD = 21,16 MeV.