Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
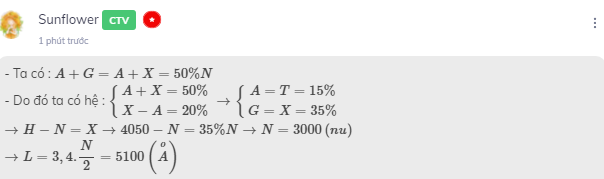
- Ta có : \(A+G=A+X=50\%N\)
- Do đó ta có hệ : \(\left\{{}\begin{matrix}A+X=50\%\\X-A=20\%\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}A=T=15\%\\G=X=35\%\end{matrix}\right.\)
\(\rightarrow H-N=X\rightarrow4050-N=35\%N\rightarrow N=3000\left(nu\right)\)
\(\rightarrow L=3,4.\dfrac{N}{2}=5100\left(\overset{o}{A}\right)\)
a) Ta có:
\(\left\{{}\begin{matrix}\text{%A+%G=50%N}\\\%A-\%G=10\%\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\%A=\%T=30\%N\\\%G=\%X=20\%N\end{matrix}\right.\)
Vì gen chứa 3600 liên kết hidro:
H=3600
<=> 2A+3G=3600
<=>2.30%N+3.20%N=3600
<=>N=3000(Nu)
Chiều dài của gen:
L=N/2 x 3,4= 3000/2 x 3,4=5100(Ao)
b) Số nu từng loại của gen:
A=T=30%N=30%.3000=900(Nu)
G=X=20%N=20%.3000=600(Nu)
1,theo NTBS, ta co tong cua 2 loai Nu khong bo sung nhau luon bang nhau va bang 50% tong so Nu cua toan phan tu.Theo đề bài ,tổng của 2 loại Nu bằng 90%chỉ có thể là tổng của 2 loại Nu bổ sung cho nhau
TH1:Nếu A+T=90%=>A=T=90%/2=45%;G=X=50%-45%=5%
TH2:Nếu G+X=90%=.G=X=90%/2=45%=>A=T=50%-45%=5%
2,-then NTBS,ta coG=X=>X-G=0
-theo đề baihieu giữa Nu loại G với 1 Nụ loại khác =30%nên chỉ có thể là hiệu giữa G với A hay T
-ta co: G-A=20%(1)
Theo NTBS;G+A=50%(2)
lay (1)+(2),=>2G=70%=>G=X=35%; A=T=50%-35%=15%
3, goi 2 loai Nu khong bo sung cho nhau la A va G
-theo đề bài , tả cô:A xG=6%=0.06 (1)
A+G=50%=0,5(2)
tu (1) va (2) =.A va G la nghiem cua phuong trinh:x2-0,5x+0,06=0
giai phuong trinh ta tim duoc x1=0,3;x2=0,2
có 2 trường hợp:A=T=30%;G=X=20% hoặc A=T=20%;G=X=30%
a) Ta có: Một gen có hiệu số phần trăm giữa nu loại G với nu loại khác là 20%
\(\Rightarrow\%G-\%A=20\%\)(1)
Theo nguyên tắc bổ xung: \(\%A+\%G=50\%\)(2)
Từ (1) và (2) suy ra hệ phương trình:\(\left\{{}\begin{matrix}\%G-\%A=20\%\\\%A+\%G=50\%\end{matrix}\right.\)
Giải hệ phương trình trên, ta được %G= 35%; %A= 15%
Gọi N là số nuclêôtit của gen(\(N\in Z^+\))
Ta có: 4050 liên kết Hiđro.
\(\Rightarrow2.15\%N+3.35\%N=4050\)
Giải phương trình trên, ta được N= 3000(nuclêôtit)
Chiều dài của gen là:
3000: 20 . 34 = 5100 (A0)
b) Số nuclêôtit của các gen con sau khi gen nhân đôi là:
3000.23 = 24000(nuclêôtit)
tổng số nu cần cung cấp cho phiên mã là:
\(\dfrac{24000}{2}.2=24000\)(nuclêôtit)
+, Trường hợp 1:
Ta có: \(\left\{{}\begin{matrix}X-A=140\\2A+3X=2520\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}X=G=560\\A=T=420\end{matrix}\right.\)
+, Trường hợp 2:
Ta có: \(\left\{{}\begin{matrix}A-X=140\\2A+3X=2520\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}X=G=448\\A=T=588\end{matrix}\right.\)
\(a,\left\{{}\begin{matrix}\%A+\%G=50\%N\\\%G-\%A=20\%N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\%A=\%T=15\%N\\\%G=\%X=35\%N\end{matrix}\right.\\ A=T=15\%N=15\%.3000=450\left(Nu\right)\\ G=X=35\%N=35\%.3000=1050\left(Nu\right)\\ b,A_{mt}=T_{mt}=A\left(2^5-1\right)=450.31=13950\left(Nu\right)\\ G_{mt}=X_{mt}=G\left(2^5-1\right)=1050.31=32550\left(Nu\right)\)
a) - Cho là hiệu G và A.
\(\left\{{}\begin{matrix}G-A=20\%N\\G+A=50\%N\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}G=35\%N\\A=15\%N\end{matrix}\right.\)
Vậy, tỉ lệ phần trăm số nu mỗi loại của gen:
A=T= 15%N
G=X=35%N
b) - Vì theo NTBS : A=T => Tỉ lệ kia là của A và G (hoặc A và X)
\(\left\{{}\begin{matrix}\dfrac{A}{G}=\dfrac{1}{7}\\A+G=50\%N\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}A=6,25\%N\\G=43,75\%N\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}A=T=6,25\%N\\G=X=43,75\%N\end{matrix}\right.\)
c) Ta có:
\(\left\{{}\begin{matrix}A+G=50\%N\\A.G=6\%N\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}A=20\%N\\G=30\%N\end{matrix}\right.\\\left\{{}\begin{matrix}A=30\%N\\G=20\%N\end{matrix}\right.\end{matrix}\right.\\ \)
TH1: A=T=20%N
G=X=30%N
TH2: A=T=30%N
G=X=20%N
Tổng số nu của gen
N=M/300 = 3000 (nu)
\(\left\{{}\begin{matrix}A-G=10\%N\\A+G=50\%N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}A=T=30\%N=900\left(nu\right)\\G=X=20\%N=600\left(nu\right)\end{matrix}\right.\)
T1 = A2 = 650 (nu)
T2 = A1 = 900 - 650 = 250 (nu)
G1 = X2 = 250 nu
G2 = X1 = 600 - 250 = 350 (nu)
