Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mạch chỉ có điện trở thuần thì u cùng pha với i.
Nếu \(u=U_0\cos\left(\omega t+\varphi\right)\)
Thì: \(i=I_0\cos\left(\omega t+\varphi\right)\)
\(\Rightarrow\frac{u}{U_0}=\frac{i}{I_0}\)
\(\Rightarrow\frac{u^2}{U_0^2}+\frac{i^2}{I_0^2}=1\) là sai.

*) Từ hai biểu thức dòng điện, rút ra 2 kết luận sau: khi \(\omega\) thay đổi thì
+) I cực đại tăng \(\frac{I_2}{I_1}=\sqrt{\frac{3}{2}}\Rightarrow \frac{Z_1}{Z_2}=\sqrt{\frac{3}{2}}\)
+) Pha ban đầu của i giảm 1 góc bằng: \(\frac{\pi}{3}-\left(-\frac{\pi}{12}\right)=\frac{5\pi}{12}=75^0\)
tức là hai véc tơ biểu diễn Z1 và Z2 lệch nhau 75 độ, trong đó Z2 ở vị trí cao hơn
*) Dựng giản đồ véc-tơ:
Trong đó: \(\widehat{AOB}=75^0\);
Đặt ngay: \(Z_1=OB=\sqrt{\frac{3}{2}}\Rightarrow Z_2=1\)
Xét tam giác OAB có \(\widehat{AOB}=75^0;OA=1;OB=\sqrt{\frac{3}{2}}\) và đường cao OH.
Với trình độ của bạn thì thừa sức tính ngay được: \(OH=\frac{\sqrt{3}}{2}\)
\(\Rightarrow R=OH=\frac{\sqrt{3}}{2}\)
*) Tính \(Z_L,Z_C\):
\(Z_1^2=R^2+\left(Z_L-Z_C\right)^2;\left(Z_L< Z_C\right)\)
\(Z_2^2=R^2+\left(\sqrt{3}Z_L-\frac{Z_C}{\sqrt{3}}\right)^2\)
Thay số vào rồi giải hệ 2 ẩn bậc nhất, tìm được: \(Z_L=\frac{\sqrt{3}}{2};Z_C=\sqrt{3}\)
*) Tính
\(\frac{R^2L}{C}=\frac{R^2\cdot\left(L\omega_1\right)}{C\omega_1}=R^2Z_LZ_C\\ =\left(\frac{\sqrt{3}}{2}\right)^2\cdot\frac{\sqrt{3}}{2}\cdot\sqrt{3}=\frac{9}{4}\)
Ra $\frac{1}{2}$ ông ạ
Thầy tôi bảo có cách dùng giản đồ vector ngắn kinh khủng mà chưa ngộ ra.

Độ lêch pha giữa u và i là: \(\Delta \varphi = \varphi_u - \varphi_i = \frac{\pi}{6} - \frac{-\pi}{3} = \frac{\pi}{2}.\)
=> u sớm pha hơn i một góc \(\pi/2\) tức là mạch AB chứa cuộn dây thuần cảm. Còn các trường hợp khác thì không có u sớm pha hơn i một góc 90 độ.
Chọn đáp án. A.

Chọn C
*Ta có thể mắc nối tiếp hoặc song song C1 và C0
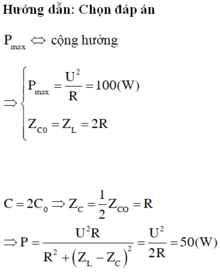
*Khi C=C0 mạch xảy ra cộng hưởng điện:
ZL=ZC0=2R ; P= U 2 2 R
Công suất tiêu thụ:
P= U 2 R 2 + ( Z L - Z C 01 ) 2 R = U 2 R R 2 + ( 2 R - Z C 01 ) 2
Khi P1=2P thì R 2 + ( 2 R - Z C ) 2 = 2 R 2
=> ZC01 = R hoặc ZC01 =3R
*Nếu ZC01 = R < ZCO = 2R => Cần mắc C1 // với C0 và có giá trị thỏa mãn:
Z C 01 = Z C 0 Z C 1 Z C 0 + Z C 1 → C 1 = C 0
Mắc C2 vào mạch thì công suất lại tăng gấp đôi tức lại quay về P2 = P. Hay ta mắc tụ C2 sao cho tổng trở bằng tổng trở khi chưa mắc C1 và C2. Khi đó cần mắc C2 nối tiếp với C01 (đã gồm C0 //C1) có giá trị bằng R
=> ZC2 = R = ZC0/2 => C2 = 2C0 (1)
*Nếu ZC = 3R
Lập luận tương tự như trên. Ban đầu mắc C1 nối tiếp với C0. Sau đó mắc C2 // cụm C01: ZC01 =R
Khi đó:
![]()
=> C2 = C0 / 3
Từ (1) và (2) chọn C

Đáp án D
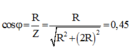
+ Hệ số công suất của đoạn mạch cos φ = R Z = R R 2 + ( 2 R ) 2 = 0 , 45

Công suất tỏa nhiệt: \(P=I^2.R=\left(\frac{I_0}{\sqrt{2}}\right)^2R=\frac{I_0^2R}{2}\)