Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Trên dây sợi dây có hai đầu cố định, xuất hiện 6 bụng sóng nên chọn n = 6.
Áp dụng công thức: \(l=n\dfrac{v}{2f}\Rightarrow0,75=6\cdot\dfrac{v}{2\cdot120}\Rightarrow v=30m/s\)
b) Tăng tốc độ truyền sóng gấp hai lần: \(v'=2v=2\cdot30=60m/s\)
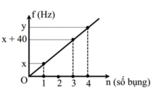
\(\Rightarrow l=n\dfrac{v'}{2f}\Rightarrow f=\dfrac{nv'}{2l}=\dfrac{n\cdot60}{2\cdot0,75}=40n\)
Với n = 1 thì f = 40 Hz
Với n = 2 thì f = 80 Hz
Với n = 3 thì f = 120 Hz
Với n = 4 thì f = 160 Hz
…
Vậy với các giá trị tần số thoả mãn f = 40 n (với n = 1; 2; 3;…) thì trên dây có sóng dừng và tốc độ truyền sóng là 60 m/s

Tham khảo:
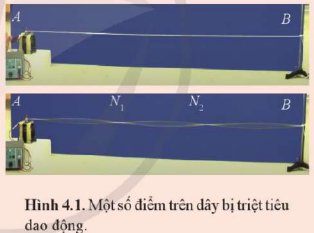
- Những điểm đứng yên này giống với những điểm đứng yên trong hiện tượng giao thoa của sóng nước.
- Tại những điểm dao động tại đó bị triệt tiêu là do sóng tới và sóng phản xạ tại điểm đó ngược pha với nhau.

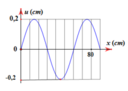
a) Ngoài đầu A, trên dây xuất hiện thêm một nút nên ta có
\(l = 3\frac{\lambda }{4} \Rightarrow \lambda = 160cm\)
Tốc độ truyền sóng là: v=f.λ=12,5.160=2000cm/s
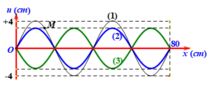
b) Để có thêm một nút sóng thì
\(l = 5\frac{\lambda }{4} \Rightarrow f = \frac{\lambda }{4}\frac{v}{{\frac{4}{5}l}} = \frac{{2000}}{{\frac{4}{5}.120}} = 20,833Hz\)






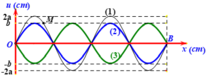

Để trên dây xuất hiện sóng dừng, ta phải có:L = \(n\frac{\lambda }{2}\) (*)
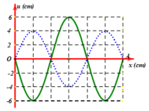
a) Trên dây xuất hiện một bụng sóng ⇒ n = 1
Thay n = 1 vào điều kiện (*) ⇒ λ = \(\frac{{2L}}{n}\) = \(\frac{{2.0,6}}{1}\)= 1,2 (m)
b) Trên dây xuất hiện ba bụng sóng ⇒ n = 3
Thay n = 3 vào điều kiện (*) ⇒ λ=\(\frac{{2L}}{n}\) = \(\frac{{2.0,6}}{3}\)= 0,4(cm)