Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện để xuất hiện sóng dừng trên dây có hai đầu cố định là L = \(n\frac{\lambda }{2}\)
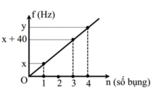
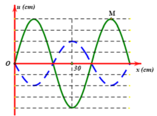
Từ hình vẽ ta thấy trên dây xuất hiện 3 bụng sóng ⇒ n = 3
⇒ λ=\(\frac{{2L}}{n}\) = \(\frac{{2.1,2}}{3}\)= 0,8 (m)
Tốc độ sóng truyền trên dây là: v = λf = 0,8.13,3 = 10,64 (m/s)

Tham khảo:
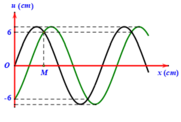
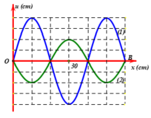
a) Trên dây sợi dây có hai đầu cố định, xuất hiện 6 bụng sóng nên chọn n = 6.
Áp dụng công thức: \(l=n\dfrac{v}{2f}\Rightarrow0,75=6\cdot\dfrac{v}{2\cdot120}\Rightarrow v=30m/s\)
b) Tăng tốc độ truyền sóng gấp hai lần: \(v'=2v=2\cdot30=60m/s\)
\(\Rightarrow l=n\dfrac{v'}{2f}\Rightarrow f=\dfrac{nv'}{2l}=\dfrac{n\cdot60}{2\cdot0,75}=40n\)
Với n = 1 thì f = 40 Hz
Với n = 2 thì f = 80 Hz
Với n = 3 thì f = 120 Hz
Với n = 4 thì f = 160 Hz
…
Vậy với các giá trị tần số thoả mãn f = 40 n (với n = 1; 2; 3;…) thì trên dây có sóng dừng và tốc độ truyền sóng là 60 m/s

Tham khảo:
Để đo được tần số của sóng âm và tốc độ truyền âm ta cần có các dụng cụ đo chuyên dụng. Ví dụ như tần số của âm thoa, hay các loại nhạc cụ thì cần có các bộ dụng cụ trong phòng thí nghiệm, dao động kí điện tử. Các loại âm thanh có tần số không xác định được phát ra từ các động cơ, máy khoan thì cần có các dụng cụ đo chuyên dụng hơn và cần sử dụng các công thức về năng lượng âm, mức cường độ âm để xác định.







a) Ta có: \(f=\dfrac{v}{2l}=\dfrac{422}{2\cdot0,64}=330Hz\)
b) Vậy trong trường hợp này thì chiều dài dây giảm 3,7 cm
\(f=\dfrac{v}{2l}=\dfrac{422}{2\cdot\left(0,64-0,037\right)}=350Hz\)