Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dây thứ nhất có: l1 = 200m, S1 = 0,2mm2, R1 = 120Ω
Dây thứ hai có: l2 = 50m, S2 = ? mm2, R2 = 45Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l3 = l2 =50m nhưng lại có tiết diện S3 = S1 = 0,2 mm2.
Như vậy dây 1 và dây 3 có cùng vật liệu và tiết diện, khác chiều dài
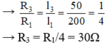
→ R3 = R1/4 = 30Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng chiều dài, khác tiết diện →
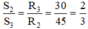
→ S2 = 2S3/3 = 2.0,2/3 = 2/15mm2 = 0,133mm2.
Lưu ý: Qua hai bài trên ta nhận thấy, với hai dây dẫn cùng vật liệu nhưng có chiều dài và tiết diện khác nhau thì ta có thể dùng hệ thức liên hệ sau để làm nhanh hơn.
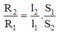

C4: Ta có: S1/S2=0,5/2,5=1/5
=>R1/R2=5
=>R2=1,1Ω
C5:
Ta có: R1/R2=(l1/S1)/(l2/S2)
=> R2=R1.(l2/S2)/(l1/S1)
=500.(50/0,5)/(100/0,1)=50Ω
C6:
R1/R2=(l1/S1)/(l2/S2)
=>S2=l2.(R1/R2)/(l1/S1)
=50.(120/45)/(200/0,2)
=0,133 mm2

Giả sử ta có một dây constantan dài l2 = 100 m, có tiết diện S2 = 0,5 mm2. So sánh dây này với dây thứ nhất ra sẽ tìm được điện trở của dây này nhỏ bằng 1/5 lần, tức là bằng 100 Ω. Giả sử cắt đôi dây này thì điện trở của nó sẽ là 50 Ω. Và đây chính là điện trở của dây dẫn cần tìm.
Giả sử ta có một dây constantan dài l2 = 100 m, có tiết diện S2 = 0,5 mm2. So sánh dây này với dây thứ nhất ra sẽ tìm được điện trở của dây này nhỏ bằng 1/5 lần, tức là bằng 100 Ω. Giả sử cắt đôi dây này thì điện trở của nó sẽ là 50 Ω. Và đây chính là điện trở của dây dẫn cần tìm.

Dây thứ nhất có: l 1 = 200m, S 1 = 1 m m 2 , R 1 = 5,6Ω
Dây thứ hai có: l 2 = ? m, S 2 = 2 m m 2 , R 2 = 16,8 Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l 3 = l 1 = 200m nhưng lại có tiết diện S 3 = S 2 = 2 m m 2 .
Như vậy dây 1 và dây 3 có cùng vật liệu và chiều dài, khác tiết diện
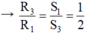
→ R 3 = R 1 /2 = 2,8Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng tiết diện, khác chiều dài
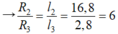
→ l 2 = 6 l 1 = 6.200 = 1200m

a. \(\left[{}\begin{matrix}R1=p1\dfrac{l1}{S1}=0,4.10^{-6}\dfrac{100}{0,5.10^{-6}}=80\left(\Omega\right)\\R2=p2\dfrac{l2}{S2}=0,4.10^{-6}\dfrac{100}{0,5S1}=0,4.10^{-6}\dfrac{100}{0,5.0,5.10^{-6}}=160\left(\Omega\right)\end{matrix}\right.\)
b. \(I=I1=I2=\dfrac{U}{R}=\dfrac{40}{80+160}=\dfrac{1}{6}\left(A\right)\left(R1ntR2\right)\)
\(\Rightarrow\left[{}\begin{matrix}U1=I1.R1=\dfrac{1}{6}.80=\dfrac{40}{3}\left(V\right)\\U2=I2.R2=\dfrac{1}{6}.160=\dfrac{80}{3}\left(V\right)\end{matrix}\right.\)

Ta có: S 1 = 5 m m 2 , S 2 = 0,5 m m 2 , suy ra S 2 = S 1 /10
Vì hai dây dẫn bằng đồng có cùng chiều dài nên ta có:
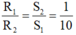

\(5,6W=5,6\Omega;16,8W=16,8\Omega\)
\(\dfrac{R_1}{R_2}=\dfrac{\dfrac{l_1}{S_1}}{\dfrac{l_2}{S_2}}=\dfrac{l_1.S_2}{S_1.l_2}\Rightarrow l_2=\dfrac{l_1.S_2}{S_1}:\dfrac{R_1}{R_2}=\dfrac{200.1.10^{-6}}{2.10^{-6}}:\dfrac{5,6}{16,8}=300\left(m\right)\)

\(R1=p1\dfrac{l1}{S1}\Rightarrow p1=\dfrac{R1\cdot S1}{l1}=\dfrac{12\cdot1\cdot10^{-6}}{200}=6\cdot10^{-8}\Omega m\)
Vì hai dây dẫn này cùng chất nên p1 = p2.
\(R2=p2\dfrac{l2}{S2}\Rightarrow l2=\dfrac{R2\cdot S2}{p2}=\dfrac{24\cdot2\cdot10^{-6}}{6\cdot10^{-8}}=800m\)
Chọn D
Lập tỉ lệ ta dc
\(\dfrac{R_1}{R_2}=\dfrac{\rho\dfrac{l_1}{S_1}}{\rho\dfrac{l_2}{S_2}}\Rightarrow\dfrac{12}{24}=\dfrac{\dfrac{200}{1\cdot10^{-6}}}{\dfrac{l_2}{2\cdot10^{-6}}}\Rightarrow l_2=800\left(m\right)\)
chọn D
Dây thứ nhất có: l1 = 100m, S1 = 0,1 mm2, R1 = 500Ω
Dây thứ hai có: l2 = 50m, S2 = 0,5 mm2, R2 = ? Ω
Ta chọn thêm dây thứ 3 cùng vật liệu với 2 dây trên sao cho có:
l3 = l1 =100m nhưng lại có tiết diện S3 = S2 = 0,5 mm2.
Như vậy dây 1 và dây 3 có cùng vật liệu và chiều dài, khác tiết diện →
→ R3 = R1/5 = 100Ω
Lại có dây 2 và dây 3 có cùng vật liệu, cùng tiết diện, khác chiều dài →
→ R2 = R3/2 = 100/2 = 50Ω