Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
f = f1. → Zd = R 2 + Z L 1 2 =100Ω => R 2 + Z L 1 2 = 10 4
Khi UC = UCmax thì ZC1 = R 2 + Z L 1 2 Z L 1 => L C = R 2 + Z L 1 2 = 10 4 (*)
Khi f = f2; I = Imax trong mạch có cộng hưởng điện => ZC2 = ZL2
LC = 1 ω 2 2 = 1 4 π 2 f 2 2 (**)
Từ (*) và (**) => L2 = 10 4 4 π 2 f 2 2 => L = 10 2 2 πf 2 = 1 2 π = 0 , 5 π H

Giải thích: Đáp án C
Khi f = f1 thì tổng trở của cuộn dây là: ![]()
Điều chỉnh điện dung của tụ sao cho điện áp trên tụ cực đại thì: [Bản quyền thuộc về website dethithpt.com]
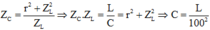
Khi f = f2 thì mạch có cộng hưởng nên: 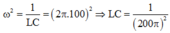
Thay 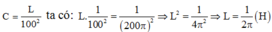

Giải thích: Đáp án A
+ Khi C = C1 , ta có: điện áp hiệu dụng giữa hai đầu tụ điện và hai đầu cuộn cảm có cùng giá trị và bằng U nên:
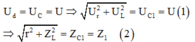
Điện áp toàn mạch khi đó:
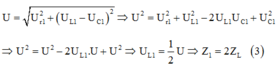
Thay vào (1), ta có: ![]()
Từ (2), (3), (4) ta có:
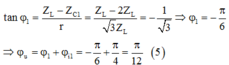
+ Khi C = C2 thì điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực đại nên
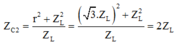
Tổng trở của mạch khi đó: ![]()
Độ lệch pha khi ZC = ZC2: 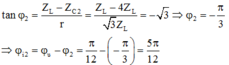
+ Áp dụng định luật Ôm cho cả hai trường hợp ta có:
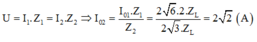
+ Biểu thức cường độ dòng điện khi ZC = ZC2:
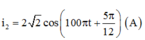

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$

Chọn B
U RL = | · Z RL = U R 2 + Z L 2 R 2 + Z L - Z C 2 ∉ R ⇔ Z L 2 = Z L - Z C 2 ⇒ Z C = 2 Z L Z = R 2 + Z L 2 = U I = 100 Ω ⇒ Z L ≤ 100 Ω ⇒ Z C = 2 Z L ≤ 200 Ω ⇒ C ≥ 1 100 π 200 = 50 π 10 - 6 F

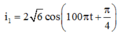
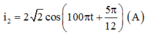
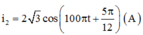
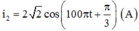
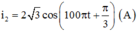
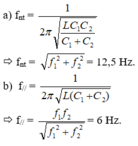
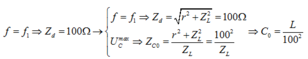
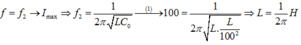
Khi C thay đổi mà I không đổi → ZL=\(\frac{ZC1+ZC2}{2}\) → Zc2=20 → C2= \(\frac{5.10^{-4}}{\Pi}\)
\(\frac{5.10^{-4}}{\Pi}=\frac{10^{-3}}{2\Pi}\) haha ,đi thi mà cho kiểu đáp án lừa nhau thế thì cg vui đấy ..