Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

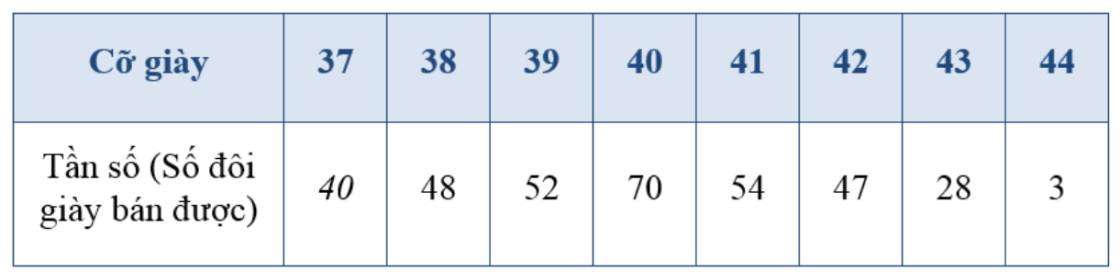
a) Ta thấy tần số lớn nhất là 70 và 70 ứng với cỡ giày 40 nên mốt của mẫu số liệu là: \({M_o} = 40\)
b) Do mốt là 40 nên cửa hàng đó nên nhập về nhiều hơn cỡ giày 40 để bán trong tháng tiếp theo.

a)
Bảng tần số:
Cỡ giày | 38 | 39 | 40 | 41 |
Số giày | 3 | 9 | 2 | 1 |
Cỡ giày trung bình:
\(\bar X = \frac{{38.3 + 39.9 + 40.2 + 41}}{{3 + 9 + 2 + 1}} = \frac{{586}}{{15}} \approx 39\)
Ý nghĩa: Cỡ giày trung bình này có thể đại diện cho cỡ giày của cửa hàng.
b) Cỡ giày số 39 là cỡ giày nhiều khách nam đi nhất trong tổng số người được chọn nên cửa hàng nên nhập cỡ giày này.

Vì không giảm giá thì cửa hàng được lãi 20%.
Khi giảm giá bán 10% 1 chiếc điện thoại, tỉ lệ của số tiền lãi lẫn vốn so với tiền vốn là:
100% + 8%=108%
Khi giảm giá bán 10% 1 chiếc điện thoại, tỉ lệ giữa số tiền nếu không giảm giá và số tiền khi giảm giá là:
100% - 10% = 90%
Nếu không giảm giá, tỉ lệ giữa số tiền lãi lẫn vốn so với tiền vốn là:
108% : 90% * 100% = 120%
Nếu không giảm giá thì cửa hàng được lãi so với tiền vốn:
120% -100% = 20%
Đáp số: 20%

Để cửa hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0 \Leftrightarrow - 3{x^2} + 200x - 2325 > 0\)
Tam thức \(I = - 3{x^2} + 200x - 2325\) có \(\Delta = 12100 > 0\), có hai nghiệm phân biệt \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
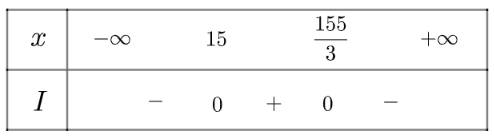
Vậy ta thấy cửa hàng có lợi nhuận khi \(x \in \left( {15;\frac{{155}}{3}} \right)\) (kg)



A
Mik đang cần gấp ,có ai làm được giúp mik với ạ