Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
+ Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh là x (phút), trên truyền hình là y (phút). Chi phí cho việc này là:800.000x + 4.000.000y (đồng)
Mức chi này không được phép vượt qúa mức chi tối đa, tức:
800.000x+ 4.000.000y ≤ 16.000.000 hay x+ 5y-20 ≤ 0
Do các điều kiện đài phát thanh, truyền hình đưa ra, ta có:x ≥ 5 và y ≤ 4
Đồng thời do x; y là thời lượng nên x; y ≥ 0
Hiệu quả chung của quảng cáo là x+ 6y.
Bài toán trở thành: Xác định x; y sao cho:
M( x; y) = x + 6y đạt giá trị lớn nhất.
Với các điều kiện : 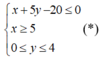
Trước tiên ta xác định miền nghiệm của hệ bất phương trình (*)
+Trong mặt phẳng tọa độ vẽ các đường thẳng
(d) : x + 5y - 20= 0 và (d’) ; x = 5; ( d’’) y = 4.
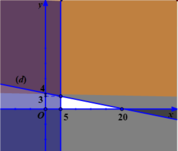
Khi đó miền nghiệm của hệ bất phương trình (*) là phần mặt phẳng(tam giác) không tô màu trên hình vẽ
Giá trị lớn nhất của M( x; y) =x+ 6y đạt tại một trong các điểm (5;3) ; ( 5;0) và ( 20; 0).
Ta có M (5; 3) = 23; M( 5; 0) = 5 và M( 20; 0) = 20.
+ Suy ra giá trị lớn nhất của M( x; y) bằng 23 tại ( 5; 3) tức là nếu đặt thời lượng quảng cáo trên sóng phát thanh là 5 phút và trên truyền hình là 3 phút thì sẽ đạt hiệu quả nhất.

a)
Nếu \(0 < x \le 2\) thì \(T(x) = 1,2x\) (triệu đồng)
Nếu \(x > 2\) thì \(T(x) = 1,2.2 + 0,9.(x - 2) = 0,9x + 0,6\) (triệu đồng)
Số tiền phải trả sau khi thuê x ngày là
\(T(x) = \left\{ \begin{array}{l}1,2x\quad \quad \quad \;(0 < x \le 2)\\0,9x + 0,6\quad (x > 2)\end{array} \right.\)
b) \(T(2) = 1,2.2=2,4\) (triệu đồng)
Ý nghĩa: số tiền khách phải trả khi thuê 2 ngày là 2,4 triệu đồng
\(T(3) = 0,9.3+0,6 = 3,3\) (triệu đồng)
Ý nghĩa: số tiền khách phải trả khi thuê 3 ngày là 3,3 triệu đồng
\(T(5) = 0,9.5+0,6=5,1\)
Ý nghĩa: số tiền khách phải trả khi thuê 5 ngày là 5,1 triệu đồng

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
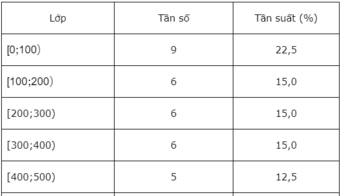
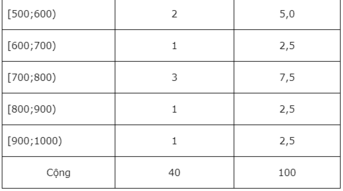
b) b) Cộng các tần suất của bốn lớp [300;400), [400;500), [500;600), [600;700) ta được 15+ 12,5+ 5+ 2,5 = 35. Đáp án là B.

Bảng số liệu có 7 giá trị, sắp các giá trị theo thứ tự không giảm ta có:
650, 670, 690, 720, 840, 2500, 3000.
Vì số phần tử = 7 là số lẻ nên số trung vị là Me = 720 (số chính giữa của dãy).
Ý nghĩa:
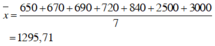
Số trung bình này chênh lệch quá lớn so với các số liệu nên không đại diện được cho các số liệu.
Trong trường hợp này, số trung vị nên được chọn làm giá trị đại diện cho mức lương.

Bước 1:
Số tiền bán x vé loại 1 là: \(x.50\) (nghìn đồng)
Số tiền bán y vé loại 2 là: \(y.100\) (nghìn đồng)
Bước 2:
Số tiền thu được là
\(50x + 100y\) (nghìn đồng)
a)
Ta có 20 triệu = 20 000 (nghìn đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50x + 100y \ge {20 000}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Vậy các số nguyên không âm x và y phải thỏa mãn điều kiện \(x + 2y \ge 400\)
b)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50x + 100y < {20 000}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Chú ý:
- Số tiền tối thiểu thì ta phải lập bất phương trình với dấu “\( \ge \)”.
- Cần đổi 20 triệu đồng thành 20 000 nghìn đồng tránh lập sai bất phương trình.

Trong 15 phút , mũi kim phút vạch cung tròn có số đo \(\frac{\pi}{2}.1,75\approx2,75\left(m\right)\) và mũi kim giờ vạch cung tròn có số đo \(\frac{\pi}{24}\)nên cung đó có độ dài là \(\frac{\pi}{24}.1,26\approx0,16\left(m\right)\)
tại sao lại là \(\frac{\pi}{2}\) và \(\frac{\pi}{24}\) hả bn ?

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
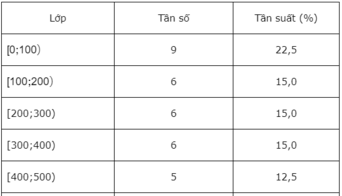
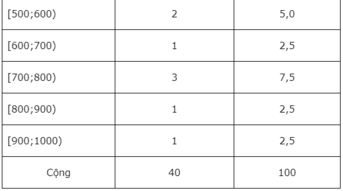
c) Cộng các tần suất của năm lớp [500;600), [600;700), [700;800), [800;900) và [900;1000) ta được . Đáp án là B.


Tham khảo
Bước 1:
Gọi x là số phút gọi nội mạng (\(x \in \mathbb{N}\)), y là số phút gọi ngoại mạng (\(y \in \mathbb{N}\))
Số tiền cần phải trả là \(x + 2y\) nghìn đồng.
Để số tiền phải trả ít hơn 200 nghìn đồng thì \(x + 2y < 200\).
Như vậy, bài toán trở thành tìm miền nghiệm của bất phương trình \(x + 2y < 200\)
Bước 2:
Xác định miền nghiệm:
+ Vẽ đường thẳng d: x+2y=200 (nét đứt).
+ Thay tọa độ O(0;0) vào biểu thức x+2y ta được 0+2.0=0<200
=> Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa gốc tọa độ không kể đường thẳng d.
Vậy nếu số phút sử dụng nội mạng là x và ngoại mạng là y mà điểm (x;y) nằm trong miền tam giác OAB không kể đoạn AB thì số tiền phải trả thấp hơn 200 nghìn đồng.
Chú ý
x và y là số tự nhiên nên cần lấy phần không âm của trục Ox và phần không âm của trục Oy.