Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a 30
\(\omega =4\pi(rad/s)\)
\(|a|\le160\sqrt 3\) ứng với phần gạch đỏ trên hình, thời gian 1/3T ứng với véc tơ quay 1 góc 1200,.
Do vậy, mỗi một góc nhỏ là 300
\(\Rightarrow a_{max}=\dfrac{a}{\sin 30^0}=2a=320\sqrt 3(cm/s) \)
\(\Rightarrow A = \dfrac{a_{max}}{\omega^2}=2\sqrt 3(cm)\)
Cơ năng: \(W=\dfrac{1}{2}kA^2\Rightarrow k=\dfrac{2W}{A^2}=\dfrac{0,004}{(0,02\sqrt 3)^2}=...\)

a) \(W_{đmax}=W\) \(\Rightarrow\frac{W_{đ1max}}{W_{đ2max}}=\frac{W_1}{W_2}=\frac{kA_1^2}{kA_2^2}=\frac{3^2}{4^2}=\frac{9}{16}\)
b) Hợp lực tác dụng lên giá đỡ bằng tổng lực đàn hồi tác dụng lên 2 lò xo
\(F=k\left(\Delta l_0+x_1\right)+k\left(\Delta l_0+x_1\right)=k\left(2\Delta l_0+x_1+x_2\right)\)
\(F max \Leftrightarrow x_1+x_2 max\)
Mà hai lò xo dao động vuông pha, cùng tần số với nhau nên \(max\left(x_1+x_2\right)=\sqrt{x_1^2+x_2^2}=0,05\left(m\right)\)
Vậy \(F_{max}=k\left(2\Delta l_0+0,05\right)=50\left(2\cdot\frac{g}{\omega^2}+0,05\right)=\frac{35}{6}\left(N\right)\)

\(F_{đh}=-k.x\Rightarrow x=\dfrac{F}{k}\)
Bảo toàn cơ năng ta có:
\(\dfrac{1}{2}mv_1^2+\dfrac{1}{2}k.x_1^2=\dfrac{1}{2}mv_2^2\) (lúc sau, lực đàn hồi = 0 thì x = 0 -> thế năng bằng 0)
\(\Rightarrow mv_1^2+k.(\dfrac{F_1}{k})^2=mv_2^2\)
Chọn C nhé bạn ![]()
\(\Rightarrow v_2^2 = v_1^2+\dfrac{F_1^2}{k.m}\)

Bạn áp dụng CT của dao động điều hòa:
\(A^2=x^2+\dfrac{v^2}{\omega^2}\)
Với \(x=\alpha.\ell\), li độ là độ dài cung của góc \(\alpha\) (tính theo rad)
\(\Rightarrow (\alpha_0.\ell)^2=(\alpha.\ell)^2+\dfrac{v^2.\ell}{g}\)
\(\Rightarrow \alpha_0^2=\alpha^2+\dfrac{v^2}{g\ell}\)
Chọn đáp án A.

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Đáp án D
Phương pháp: Thế năng đàn hồi : Thế năng đàn hồi :
Cách giải:
Độ dãn của lò xo tại vị trí cân bằng: ![]()
Biên độ dao động của con lắc: A = 7,5 - Δl0 = 7,5 - 2,5 = 5cm
Ta có: Δl0< A
Chọn chiều dương hướng xuống
=> Vị trí lực đàn hồi có độ lớn nhỏ nhất là vị trí lò xo hông giãn cũng hông nén: Δl = 0
Thế năng đàn hồi tại vị trí đó: 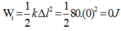

Tại vị trí cân bằng ta có \(v=v_{max}=1=\sqrt{2gl(1-\cos \alpha_0)} \Rightarrow \cos\alpha_0=\dfrac{9}{10}\)
Tại vị trí cao nhất góc lệch sợi dây là \(\alpha = \alpha_0\)
Lực căng dây:
\(T=mg(3\cos\alpha-2\cos\alpha_0)=mg(3\cos\alpha_0-2\cos\alpha_0)=mg\cos\alpha_0\)
\(\Rightarrow T = 0,25.10.\dfrac{9}{10}=2,25(N)\)

Giải thích: Đáp án D
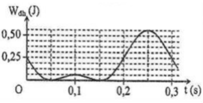
Phương pháp: Sử dung̣ lý thuyết về thế năng đàn hồi của con lắc lò xo kết hợp kĩ năng đọc đồ thi ̣
Cách giải:
+ Bài này đã chọn mốc thế năng tại vị trí lò xo không biến dạng.
+ Từ đồ thị => Wtdh có độ chia nhỏ nhất: 0,25/4 = 0,0625 J.
+ Tại vị trí cao nhất thế năng đàn hồi:
+ Tại vị trí thấp nhất thế năng đàn hồi cực đại:
+ Lấy (2) chia (1):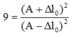
+ Từ đồ thị Chu kì dao động của con lắc: T = 0,3 s.
+ Ta có: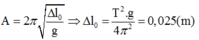
+ Tại VTCB: