

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Con lắc dao động điều hòa theo phương thẳng đứng
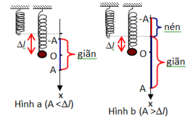
Từ đồ thị => gốc thế năng đàn hồi ở vị trí lò xo có độ dài tự nhiên và thuộc trường hợp A>Δl
Từ đồ thị ta có mỗi dòng ngang có mức thế năng: 0,25 /4 = 0,0625J.
Ta có, thế năng đàn hồi của lò xo: W t = 1 2 k x 2 (x là độ biến dạng của lò xo so với vị trí lò xo có độ dài tự nhiên). Từ đồ thị ta thấy:
+ Tại vị trí lò xo không biến dạng: Wt = 0
+ Tại vị trí vật lên cao nhất: x= A-Δl -> thế năng đàn hồi:
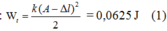
+ Tại vị trí vật xuống thấp nhất:x= A+Δl -> thế năng đàn hồi cực đại :
![]()
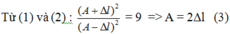
+ Chu kì dao động của con lắc:T= 0,3s
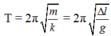
![]()
Suy ra A =2Dl0 = 4,5cm. Từ k ( A - ∆ l ) 2 2 = 0 , 0625
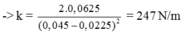
Từ T = 2 π m k
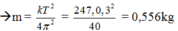

Tại VTCB : đental = 2.5cm
biên độ : A=(30 - 20)/2 = 5cm
vậy thời gian cần tính là t = T/4 + T/12
0k???
Bài 2 hỏi độ lớn của vật là cái j hả??????
Bai 3. oomega = 20rad/s
tại VTCB denta l = g/omega^2 = 2,5cm
A = 25 - 20 - 2,5 = 2,5cm
li độ tại vị trí lò xo có chiều dài 24cm x=24-22,5 = 1,5cm
Áp dụng CT độc lập với thời gian ta tính được v = 40cm/s
từ đó suy ra động năng thui

Vật ở VTCB lò xo giãn ra một đoạn: \(\Delta l\)
\(\Rightarrow\Delta l=\frac{g}{\omega^2}\Leftrightarrow\omega\sqrt{\frac{g}{\Delta l}}\)
Tần số của con lắc lò xo:
\(\Rightarrow f=\frac{\omega}{2\pi}=\frac{1}{2\pi}\sqrt{\frac{g}{\Delta l}}\)

\(T=2\pi\sqrt{\frac{\Delta l_0}{9}}=0,4s\)
\(\Rightarrow\Delta l_0=4=\frac{A\sqrt{2}}{2}\)
Thời gian lò xo không giãn là \(t=2t-\frac{A\sqrt{2}}{2}\Rightarrow-A=\frac{T}{4}=0,10\left(s\right)\)
Vậy D đúng

Vận tốc của hai vật sau va chạm: (M + m)V = mv
=> V = 0,02\(\sqrt{2}\) (m/s)
Tọa độ ban đầu của hệ hai vật x0 = \(\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}\) = 0,04m = 4cm
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2+\left(M+m\right)}{k}=0,0016\Rightarrow A=0,04m=4cm\)
→ B
Vận tốc của hai vật sau va chạm: \(\left(M+m\right)V=mv\)
\(\rightarrow V=0,02\sqrt{2}\left(m\text{ /}s\right)\)
Tọa độ ban đầu của hệ hai vật: \(x_0=\frac{\left(M+m-M\right)g}{k}=\frac{mg}{k}=0,04m=4cm\)
\(A^2=x_0^2+\frac{V^2}{\omega^2}=x_0^2+\frac{V^2\left(M+m\right)}{k}=0,0016\) \(\rightarrow A=0,04m=4cm\)
Đáp án B