Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+ W t 2 W t 1 = 3 s 2 s 2 = 9 − W − W d 2 W − W d 1 ⇒ W = 9 W d 1 − W d 2 8 = 0 , 125 J
+ Nếu đi thêm đoạn s nữa: W t 3 W t 1 = 4 s 2 s 2 = 16 = W − W d 3 W − W d 1 ⇒ W d 3 = 16 W d 1 − 15 W = 0 , 045 J
Chọn đáp án B

Đáp án C
Lời giải chi tiết:
Sơ đồ hóa bài toán:
Quan trọng nhất của bài toán này là bảo toàn năng lượng:
![]()
Ta có
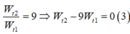
![]()
Giải (3) và (4)
![]()
Bây giờ để tính W d 3 ta cần tìm W t 3
Dựa vào 4 phương án của bài ta nhận thấy W d 3 > W d 2 = 0 , 019 ⇒ chất điểm đã ra biên và vòng trở lại.
Ta có vị trí 3S→biên A (A – 3S) rồi từ A đến vị trí 3S(A – 3S) sau cùng đi được thêm 1 đoạn nửa.
Gọi x là vị trí đi được quãng đường S cách vị trí cân bằng O
Ta có: ![]()
Lại có 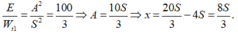
Xét 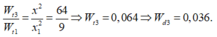

Sơ đồ hóa bài toán:
- Quan trọng nhất của bài toán này là bảo toàn năng lượng:
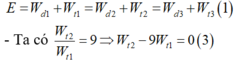
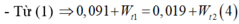
- Giải (3) và (4) :
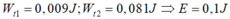
- Bây giờ để tính Wd3 ta cần tìm Wt3 = ?
- Dựa vào 4 phương án của bài ta nhận thấy Wd3 > Wd3 = 0,019 => chất điểm đã ra biên và vòng trở lại.
- Ta có vị trí 3S → biên A (A – 3S) rồi từ A đến vị trí 3S(A – 3S) sau cùng đi được thêm 1 đoạn nửa.
- Gọi x là vị trí đi được quãng đường S cách vị trí cân bằng O. Ta có:
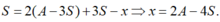
+ Lại có:
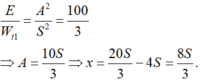
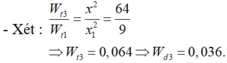

W = 1 2 k S 2 + 0 , 091 = 1 2 k ( 2 S ) 2 + 0 , 019 → 1 2 k S 2 = 0 , 024 → W = 0 , 024 + 0 , 091 = 0 , 115 J
+ Vật qua vị trí cân bằng có Wđmax = W = 0,115 ≈ 0,1 J
ü Đáp án D

+ Ta có: W d 1 = W − 1 2 k x 1 2 = 0 , 091 ( 1 ) W d 2 = W − 1 2 k 3 x 1 2 = 0 , 019 ( 2 )
+ Từ (1) và (2) ta được: 1 2 k x 1 2 = 0 , 009
+ Khi qua vị trí cân bằng động năng đạt cực đại là:
W d max = W = W d 1 + W t 1 = 0 , 091 + 0 , 009 = 0 , 1 J.
Đáp án D

ü Đáp án D
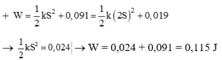
+ Vật qua vị trí cân bằng có Wđmax = W = 0,115 ≈ 0,1 J

Chọn C
Động năng của vật: W d = W − k x 2 2 8 = W − k S 2 2 5 = W − 4. k S 2 2
⇒ W = k A 2 2 = 9 m J k S 2 2 = 1 ( m J ) ⇒ S = A 3
hi đi được quãng đường 3 , 5 S = A + A 6 thì vật lúc này có độ lớn của li độ: x = A − A 6 = 5 A 6
⇒ W d = W − k x 2 2 = k A 2 2 − 25 36 k A 2 2 = 11 36 W = 2 , 75 ( J )
+K
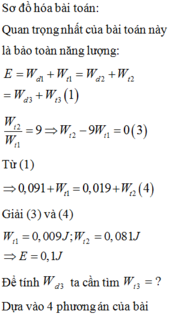

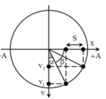

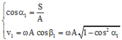
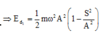


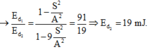
Chọn A