Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Áp dụng hệ thức độc lập với thời gian của li độ và vận tốc
Cách giải:
Áp dụng hệ thức độc lập:
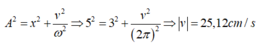

Chọn A
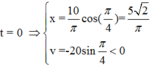
+ Thời điểm vật có vận tốc v= 20 cm/s = vmax => vật ở vị trí cân bằng x = 0.
+ Thời gian vật từ 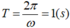 chuyển động theo chiều âm về đến x = 0 tiếp tục chuyển động tới x = -A rồi quay về x = 0 để v = +20cm/s là
chuyển động theo chiều âm về đến x = 0 tiếp tục chuyển động tới x = -A rồi quay về x = 0 để v = +20cm/s là 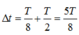 mà
mà ![]()
=> Thời gian ngắn nhất kể từ lúc bắt đầu chuyển động đến thời điểm vật có vận tốc v = 20 cm/s là 5/8 (s).

Đáp án D
Phương pháp: Sử dụng lí thuyết về lực đàn hồi trong dao động điều hòa của CLLX ngang và đường tròn lượng giác
Cách giải:
+ Đối với CLLX ngang thì lực đàn hồi đổi chiều tại VTCB
+ Biểu diễn trên đường tròn lượng giác :
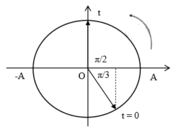
Góc quét được:
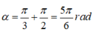
=> Từ t = 0 thì vật đi qua VTCB lần đầu tại thời điểm:
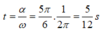

Chọn đáp án D
Tốc độ trung bình trong một chu kì:
v ¯ = S △ t = 4 A T = 4. A ω 2 π = 4.5.2 π 2 π = 20 ( c m / s ) .

Đáp án A
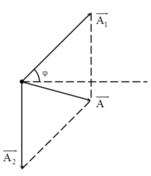
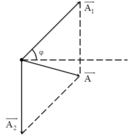
Từ hình vẽ, áp dụng định lý hàm cos trong tam giác ta có:
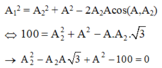
Phương trình trên luôn có nghiệm nên:

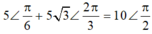

Ta có: \(F=-k.x\)
\(\Rightarrow x = -\dfrac{F}{k}=-0,05\cos(2\pi t-\dfrac{5\pi}{6})(m)\)
Vận tốc: \(v=v'_{(t)}=0,1.\pi.\sin(2\pi t-\dfrac{5\pi}{6})\)(m/s)
Đến đây chưa xong nha
Bạn phải biến đổi tiếp từ x = -0,05.cos(2πt - \(\dfrac{5\pi}{6}\)) = 0,05.cos(2πt - \(\dfrac{\pi}{6}\))(m)
=> x = 5.cos(2πt - \(\dfrac{\pi}{6}\)) (cm)
=> v = 10π.sin(2πt - \(\dfrac{\pi}{6}\)) = 10π.cos(2πt + \(\dfrac{2\pi}{3}\)) < Đây mới là đáp án cuối cùng nha>