Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C
? Lời giải:
+ Xe chuyển động chậm dần đều nên a không đổi.
+ Gọi v0 là vận tốc của xe trước thời điểm dừng lại 1 s
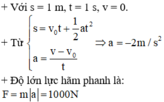

Bài 1 :
+ Xe chuyển động chậm dần đều nên a không đổi.
+ Gọi v0 là vận tốc của xe trước thời điểm dừng lại 1 s
+ Với : \(s=2,5\left(m\right);1=1s;v=0\)
\(\left\{{}\begin{matrix}s=v_0t+\dfrac{1}{2}at^2\\a=\dfrac{v-v_0}{t}\end{matrix}\right.\Rightarrow a=-5\left(\dfrac{m}{s^2}\right)\)
Lực hãm phanh :
\(F_h=m.\left|a\right|=750.5=3750\left(N\right)\)

Ta có v 2 − v 0 2 = 2 as ↔ − v 0 2 = 2 as=3,6a (1)
Mặt khác a = v − v 0 Δ t → − v 0 = a t = 2 a (2)
Từ (1) và (2) ta suy ra:a=−0,9m/s2
Lực hãm phanh tác dụng lên ôtô:F=m.a=−450N
Đáp án: C

Quãng đường đi được trong thời gian $t$ (giây) và $(t-1)$ giây đầu tiên là: $S=v_{o}t+\frac{1}{2}at^2$ và $S’=v_{o}(t-1)+\frac{1}{2}a(t-1)^2$.
Quãng đường đi được trong giây cuối cùng: $\Delta S=S’-S=1,5m$.
$\Rightarrow v_{o}t+\frac{1}{2}at^2-v_{o}(t-1)+\frac{1}{2}a(t-1)^2=v_{o}+at-\frac{a}{2}=1,5m$.
Chú ý: $at=-v_{o} \rightarrow a=-3m/s^2 \rightarrow $
Lực hãm $F=ma=950.3 = 2850N$

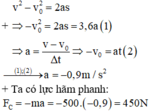
Gọi t là thời gian đi hết quãng đường
\(\left\{{}\begin{matrix}v_0t+\frac{1}{2}at^2-v_0\left(t-1\right)-\frac{1}{2}a\left(t-1\right)^2=1\\a=\frac{v-v_0}{t}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\frac{1}{2}at^2+v_0-\frac{1}{2}at^2+at-\frac{1}{2}a=1\\v_0+at=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}v_0+at-\frac{1}{2}a=1\\v_0+at=0\end{matrix}\right.\)
\(\Leftrightarrow-\frac{1}{2}a=1\Leftrightarrow a=-2\left(m/s^2\right)\)
=> \(F_h=\left|m.a\right|=\left|500.\left(-2\right)\right|=1000\left(N\right)\)