Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do 4 đỉnh hình vuông nằm trên 2 đường thẳng song song nên độ dài cạnh hình vuông chính là khoảng cách giữa hai đường thẳng song song
Ta có: d2: - x + 2y + 10= 0 hay 2x – 4y – 20 = 0
Khoảng cách hai đường thẳng là: d ( d 1 ; d 2 ) = 1 − ( − 20 ) 2 2 + ( − 4 ) 2 = 21 20
Diện tích hình vuông cần tính là: S = 21 20 2 = 441 20
ĐÁP ÁN D.

Giả sử đường thẳng ∆ song song với d : 3x- 4y+2= 0
Khi đó ; ∆ có phương trình là ∆ : 3x-4y +C= 0.
Lấy điểm M( -2 ; -1) thuộc d.

Do đó ; 2 đường thẳng thỏa mãn là:3x – 4y + 7 = 0 và 3x – 4y – 3 = 0
Chọn B

Đáp án C
Đường tròn (C) có tâm I( -1 ; 3) và bán kính R= 2
Do d’// d nên phương trình của d’ có dạng : 3x- 4y + c= 0.
Để d’ chắn trên (C) một dây cung có độ dài lớn nhất thì d’ phải đi qua tâm I của đường tròn ( trong các dây của đường tròn dây lớn nhất là đường kính).
Do I( -1 ; 3) thuộc d’ nên : 3.(-1) – 4.3 +c= 0
=> c = 15
Vậy đường thẳng cần tìm là d’ : 3x- 4y + 15= 0.

Đường thẳng song song d nên nhận (3;-4) là 1 vtpt
Phương trình:
\(3\left(x-2\right)-4\left(y-1\right)=0\Leftrightarrow3x-4y-2=0\)

Ta thấy: điểm A không thuộc hai đường thẳng trên.
Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ A đến hai đường thẳng trên.
Độ dài 2 cạnh là:
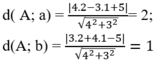
do đó diện tích hình chữ nhật bằng : S= 2.1= 2
Chọn B.

Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)

Lời giải:
Vì PTĐT cần tìm song song với $(\Delta)$ nên nó có dạng:
$3x-4y+m=0$
Khoảng cách từ $M$ đến đt cần tìm là:
$\frac{|3.2-4.(-2)+m|}{\sqrt{3^2+4^2}}=2$
$\Leftrightarrow |m+14|=10$
$\Rightarrow m=-4$ hoặc $m=-24$
Vậy PTĐT cần tìm là: $3x-4y-4=0$ hoặc $3x-4y-24=0$

Đường thẳng \(\Delta\) nhận (3;-4) là 1 vtpt
a. Do \(d_1||\Delta\) nên \(d_1\) cũng nhận (3;-4) là 1 vtpt
Phương trình d1:
\(3\left(x-2\right)-4\left(y-5\right)=0\Leftrightarrow3x-4y+14=0\)
b. Do d2 vuông góc \(\Delta\) nên d2 nhận (4;3) là 1 vtpt
Phương trình d2:
\(4\left(x-2\right)+3\left(y-5\right)=0\Leftrightarrow4x+3y-23=0\)