Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có : T=2pi/10pi=0.2(s)
Khi t=0 => vật đang ở biên âm.
Quãng đường vật đi được là : S=12.5=2A+ A/2
Xét trong quãng đường 2A,=> t1=T/2 =0.1s ( ta luôn luôn có được biểu thức T/2 = 2A)
Xét trong quãng đường A/2 : khi vật đi được 2A thì vật đang ở biên dương , đi thêm A/2 => góc quét được là pi/3 => t2=T/6 =0.2/6=1/30(s)
=> t=0.1 + 1/30=2/15 (s)
hay ghê, tui tưởng đâu chép trên mạng l à không được tick chớ

\(A^2=x^2+\frac{v^2}{\omega^2}\)
\(\frac{v^2_{max}}{\omega^2}=0.03^2+\frac{0.4^2}{\omega^2}\)
Vận tốc ở vị trí cân bằng tức là \(v_{max}=A\omega=0,5\)(m/s).
=>\(\frac{0.5^2}{\omega^2}=0.03^2+\frac{0.4^2}{\omega^2}\)
=> \(\omega=10\)(rad/s).

Phương pháp: Khoảng cách giữa hai điểm sáng được biểu diễn bởi phương trình:
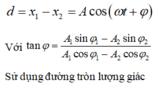
Cách giải:
+ Phương trình vận tốc của hai chất điểm:
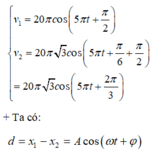
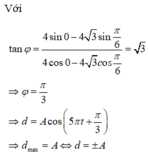
+ Thời điểm đầu tiên t hai điểm sáng cách xa nhau nhất được biểu diễn trên đường tròn lượng giác
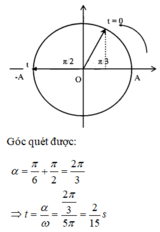
+ Tại t = 2/15s tỉ số vận tốc của chất điểm 1 so với chất điểm 2:
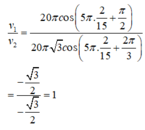
Đáp án A

Trong khoảng thời gian tỉ số giữa tốc độ trung bình nhỏ nhất và tốc độ trung bình lớn nhất cũng chính là tỉ số giữa quãng đường đi được nhỏ nhất và quãng đường đi được lớn nhất:
Smax = 3A
Smin = (4 - )A
Vậy: kết quả là

Vận tốc có giá trị dương: Vật đi từ trái sang phải
Vận tốc có giá trị đang giảm: Đi hướng ra biên
--> Vận tốc có giá trị dương và đang giảm ứng với véc tơ quay từ M đến N.
Góc quay: 600
Thời gian: \(\dfrac{60}{360}T=\dfrac{1}{6}.\dfrac{1}{2}=\dfrac{1}{12}s\)

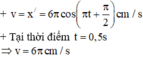
Ta có: \(x=0,3\cos\left(10\pi t\right)cm\)
Chu kì \(T=\frac{2\pi}{10\pi}=\frac{1}{5}s=0,2s\)
Tách \(1,5s=7.0,2+0,1=7T+\frac{T}{2}\)
Trong 7 chu kì đầu, vật đi đc quãng đường: 7. 4A
Trong T/2 thời gian còn lại vật đi thêm quãng đường: A (Do pha ban đầu là 0 nên bạn dễ dàng tìm đc khi biểu diễn bằng véc tơ quay)
Vậy tổng quãng đường vật đi dc: 7.4A + A = 29A = 29.0,3 = 8,7 cm