Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Ta để ý rằng, trong dao động điều hòa thì li độ và vận tốc luôn vuông pha nhau
+ Hai thời điểm t 1 và t 2 vuông pha nhau do vậy v 2 sẽ ngược pha với x 1 , ta có v 2 x 1 = b x 1 = ω = π rad.
Tương tự, thời điểm t 3 ngược pha với t 2 nên ta có
v 3 v 2 = 1 ⇔ b + 8 π b = 1 ⇒ b + 8 π b = − 1 ⇒ b = − 4 π
Thay vào biểu thức trên ta tìm được x 1 = 4 cm

Chọn đáp án A
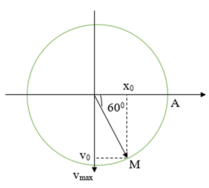
Chu kì dao động của vật:
T = 2 ( t 2 − t 1 ) = 1 , 5 s
v t b = 2 A Δ t ⇒ A = v t b Δ t 2 = 6 c m
Thời điểm t 1 = 1,75s ứng với góc
Δ φ = ω t 1 = 7 π 3 = 2 π + π 3 .
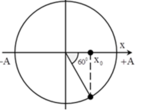
Giả sử thời điêm t 1 vật đang ở biên dương, sử dụng quay ngược lại trước đó 7 π / 3 rad ta xác định được thời điểm t 0 như hình vẽ. Từ đó ta suy ra:
x 0 v 0 = A 2 3 2 v max = 3 4 ω A 2 = 12 π 3

Đáp án B
+ Áp dụng hệ thức độc lập thời gian giữa vận tốc và gia tốc, ta có:
v 1 ωA 2 + a 1 ω 2 A = 1 v 2 ωA 2 + a 2 ω 2 A = 1 → 10 3 ωA 2 + − 100 ω 2 A 2 = 1 − 10 ωA 2 + − 3 . 100 ω 2 A 2 = 1
→ ω = 10 A = 2
+ Li độ x 2 của vật tại thời điểm t 2 :
x 2 = A 2 − v 2 ω 2 = 2 2 − − 10 10 2 = 3

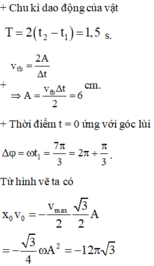
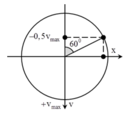
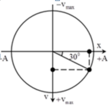

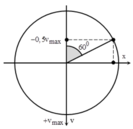



Giả sử M và N là 2 vị trí của chất điểm ở thười điểm t1 và t2.Dễ thấy t2 hơn t1 \(1/4\) chu kì nên \(\widehat{MON}=90^o\Rightarrow\widehat{AOM}+\widehat{A'ON}=90^o\)
Ta có:\(\cos^2\widehat{AOM}+\cos^2\widehat{A'ON}=cos^2\widehat{AOM}+sin^2\widehat{AOM}=1\)
\(\Rightarrow\dfrac{x_1^2}{A^2}+\dfrac{x_2^2}{A^2}=1\). Kết hợp với \(A^2=x_1^2+\dfrac{v_1^2}{\omega^2}=x_2^2+\dfrac{v_2^2}{\omega^2}\)
\(\Rightarrow x_1^2=\dfrac{v_2^2}{\omega^2}\Rightarrow v_2=\left|x_1\right|.\dfrac{2\pi}{T}=4\pi\)(\(cm/s\))
Do chọn \(OA\equiv Ox\) làm chiều dương nên \(v_2\) sẽ dương