Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Theo đề bài, ta có dãy số chỉ chiều dài các thanh ngang của cái thang đó là một cấp số cộng có số hạng đầu là \(u_1=45\), số hạng cuối \(u_n=31\) và công sai \(d=-2\)
Ta có;
\(u_n=u_1+\left(n-1\right)d\\ \Leftrightarrow31=45+\left(n-1\right)\cdot\left(-2\right)\\ \Leftrightarrow n=8\)
Vậy cái thang đó có 8 bậc.
b, Chiều dài thanh gỗ mà người đó cần mua chính là tổng của 8 thanh ngang của cái thang đó.
Vậy chiều dài thanh gỗ mà người đó cần mua là:
\(S_8=\dfrac{8\cdot\left(u_1+u_8\right)}{2}=\dfrac{8\cdot\left(45+31\right)}{2}=304\left(cm\right)\)

Các mặt của bậc thang đều song song với mặt sàn nên chúng đôi một song song với nhau.
Mặt phẳng tường cắt các mặt bậc thang tại các mép nằm trên bờ tường nên chúng song song với nhau.

Đáp án A
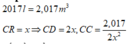
Số tiền để xây đáy là: ![]()
Số tiền để xây thân bể là: 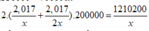
Số tiền để xây nắp bể là : ![]()
Số tiền để xây bể là :
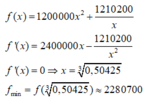

a) Mỗi bậc thang cao 16cm = 0,16m.
Do đó, n bậc thang cao 0,16n (m).
Vì mặt sàn cao hơn mặt sân 0,5m nên công thức tính độ cao của bậc n so với mặt sân là:
\({h_n} = \left( {0,5 + 0,16n} \right)\) (m)
b) Độ cao của sàn tầng hai so với mặt sân tương ứng với \(n = 25\) là:
\({h_{25}} = 0,5 + 0,16 \times 25 = 4,5\) (m)

Tham khảo:
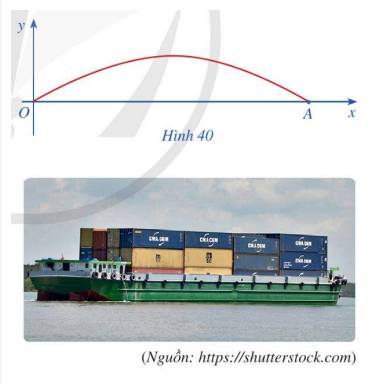
a) Hai vị trí \(O\) và \(A\) là hai vị trí chân cầu, tại hai vị trí này ta có: \(y = 0\)
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 0 \Leftrightarrow \sin \frac{x}{9} = 0 \Leftrightarrow \frac{x}{9} = k\pi (k \in \mathbb{Z}) \Leftrightarrow x = 9k\pi (k \in \mathbb{Z})\)
Quan sát đồ thị ta thấy, đồ thị hàm số \({\rm{y}} = 4,8 \cdot \sin \frac{x}{9}\) cắt trục hoành tại điểm 0 và \({\rm{A}}\) liên tiếp nhau với \(x \ge 0\).
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} = 0\);
Xét \({\rm{k}} = 1\), ta có \({{\rm{x}}_2} = 9\pi \).
Mà \({x_1} = 0\) nên đây là hoành độ của 0 , do đó \({x_2} = 9\pi \) là hoành độ của điểm \(A\).
Khi đó \(OA = 9\pi \approx 28,3\).
Vậy chiều rộng của con sông xấp xỉ 28,3 m.
b) Do sà lan có độ cao 3,6 m so với mực nước sông nên khi sà lan đi qua gầm cầu thì ứng với \({\rm{y}} = 3,6\).
\( \Leftrightarrow 4,8 \cdot \sin \frac{x}{9} = 3,6 \Leftrightarrow \sin \frac{x}{9} = \frac{3}{4} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\frac{{\rm{x}}}{9} \approx 0,848 + {\rm{k}}2\pi }\\{\frac{{\rm{x}}}{9} \approx \pi - 0,848 + {\rm{k}}2\pi }\end{array}} \right.\)
(Dùng máy tính cầm tay (chuyển về chế độ “radian”) bấm liên tiếp \(SHIFT\)\sin 3 \div 4 = ta được kết quả gần đúng là 0,85) \( \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{\rm{x}} \approx 7,632 + 18{\rm{k}}\pi }\\{{\rm{x}} \approx 9\pi - 7,632 + 18{\rm{k}}\pi }\end{array}({\rm{k}} \in \mathbb{Z})} \right.\)
Xét \({\rm{k}} = 0\), ta có \({{\rm{x}}_1} \approx 7,632;{{\rm{x}}_2} \approx 20,642\).
Ta biểu diễn các giá trị \(x\) vừa tìm được trên hệ trục tọa độ vẽ đồ thị hàm số \(y = \) 4,8. \(\sin \frac{x}{9}\) như sau:
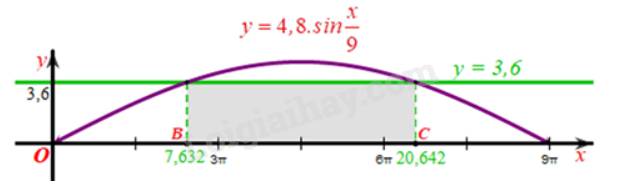
Khi đó để sà lan có thể đi qua được gầm cầu thì khối hàng hóa có độ cao 3,6 m phải có chiều rộng nhỏ hơn độ dài đoạn thẳng \({\rm{BC}}\) trên hình vẽ.
Mà \(BC \approx 20,642 - 7,632 = 13,01(m) < 13,1(m)\).
Vậy chiều rộng của khối hàng hoá đó phải nhỏ hơn 13,1 m.
c) Giả sử sà lan chở khối hàng được mô tả bởi hình chữ nhật MNPQ:
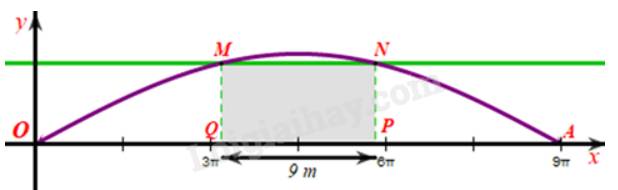
Khi đó \(QP = 9;OA = 28,3\) và \(OQ = PA\).
Mà \(OQ + QP + PA = OA \Rightarrow OQ + 9 + OQ \approx 28,3 \Rightarrow OQ \approx 9,65\)
Khi đó \({y_M} = 4,8 \cdot \sin \frac{{{x_M}}}{9} = 4,8 \cdot \sin \frac{{OQ}}{9} \approx 4,8 \cdot \sin \frac{{9,65}}{9} \approx 4,22(\;{\rm{m}}) < 4,3\) (m).
Vậy để sà lan có thể đi qua được gầm cầu thì chiều cao của khối hàng hoá đó phải nhỏ hơn 4,3 m.

Độ cao tầng hai so với mặt sàn là h = (0,5+ 0,18n) (m) với n = 21. Vậy ta có độ cao tầng 2 bằng 4,28m
Đáp án B




Để tính giá thành làm cầu thang, ta cần tính diện tích của từng bậc thang và sau đó cộng lại.
Diện tích của một bậc thang có thể tính bằng công thức: Diện tích = Chiều dài x Chiều rộng.
Ta có thể tính diện tích của từng bậc thang như sau:
Bậc đầu tiên: Diện tích = 189cm x 35cm = 6615cm² Bậc thứ hai: Diện tích = (189cm - 7cm) x 35cm = 6230cm² Bậc thứ ba: Diện tích = (189cm - 2*7cm) x 35cm = 5845cm² ... Bậc cuối cùng: Diện tích = 63cm x 35cm = 2205cm²
Sau đó, ta cộng lại diện tích của từng bậc thang để tính tổng diện tích cầu thang:
Tổng diện tích = 6615cm² + 6230cm² + 5845cm² + ... + 2205cm²
Để tính giá thành của cầu thang, ta nhân tổng diện tích cầu thang với giá thành một mét vuông:
Giá thành = Tổng diện tích x 1250000 đồng/m²
Vì không có thông tin cụ thể về số bậc thang trong câu hỏi, nên không thể tính được tổng diện tích và giá thành chính xác. Tuy nhiên, để xác định giá thành gần với số nào dưới đây, ta có thể ước lượng giá thành bằng cách lấy diện tích trung bình của các bậc thang và nhân với số bậc thang.
Giả sử số bậc thang là n, ta có:
Diện tích trung bình = (6615cm² + 6230cm² + 5845cm² + ... + 2205cm²) / n
Giá thành ước lượng = Diện tích trung bình x 1250000 đồng/m²