Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
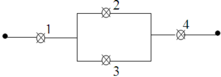
Để hoạt động tốt, mạch điện có thẻ có các trường hợp sau:
TH1: 1 tốt, 2 tốt,3 tốt, 4 tốt: P1 = 0,8.0,9.0,95.0,98 = 0,67032
TH2: 1 tốt, 2 tốt,3 cháy, 4 tốt: P1 = 0,8.0,9.0,05.0,98 = 0,03528
TH3: 1 tốt, 2 cháy,3 tốt, 4 tốt: P1 = 0,8.0,1.0,95.0,98 = 0,07448
Từ đó xác suất để mạch hoạt động tốt là 0,67032 + 0,03528 + 0,07448 = 0,78008

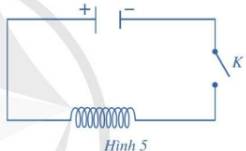
Công thức tổng quát của cường độ dòng điện tại thời gian t là:
\(I\left(t\right)=q'\left(t\right)=Q_0\cdot\omega\cdot cos\left(\omega t\right)\)
=>\(I\left(6\right)=10^{-8}\cdot10^6\cdot\pi\cdot cos\left(10^6\cdot pi\cdot6\right)=0.01\pi\left(A\right)\)

Xác suất để linh kiện 1 hoạt động tốt là: 1-0,2=0,8
Xác suất để linh kiện 2 hoạt động tốt là: 1-0,1=0,9
Xác suất để linh kiện 3 hoạt động tốt là: 1-0,05=0,95
Lưu ý rằng khi mắc mạch song song, linh kiện 1 hỏng thì linh kiện 2 vẫn hoạt động tốt và ngược lại.
Xác suất để cả 3 linh kiện hoạt động tốt là: 0 , 8.0 , 9.0 , 95 = 0 , 684
Xác suất để linh kiện 1 hỏng, 2 linh kiện còn lại hoạt động tốt là: 0 , 2.0 , 9.0 , 95 = 0 , 171
Xác suất để linh kiện 2 hỏng, 2 linh kiện còn lại hoạt động tốt là: 0 , 8.0 , 1.0 , 95 = 0 , 076
Vậy xác suất để mạch hoạt động được là: 0 , 684 + 0 , 171 + 0 , 076 = 0 , 931
Chọn đáp án A.

Không gian mẫu: \(n\left(\Omega\right)=10!\)
Chọn 5 chữ số từ 6 chữ số còn lại (khác 0,3,6,8): có \(C_6^5\) cách
Hoán vị 6 chữ số (5 chữ số được chọn nói trên và số 8): \(6!\) cách
Tổng cộng: \(6!.C_6^5\) số
Xác suất: \(P=\dfrac{6!.C_6^5}{10!}=...\)

Tham khảo
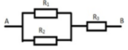
Xét sơ đô mạng điện, trong đó mỗi công tắc có 2 trạng thái đóng và mở .Hỏi mạng điện có bao nhiêu cách đóng - mở 9 công tắc trên để thông mạch từ A đến B ( tức là có dòng điện đi từ A đến B ) ? - Tìm với Google