Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
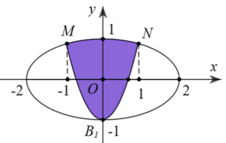
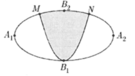
Phương trình đường Elip là: x 2 4 + y 2 1 = 1 . Diện tích hình Elip là S ( B ) = πa . b = 2 π ( m 2 )
Tọa độ giao điểm M, N là nghiệm hệ: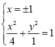 
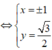
Vậy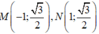 
Parabol (P) đối xứng qua Oy có dạng y = a x 2 + c a # 0
Vì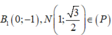 
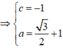
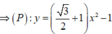
Diện tích phần tô đậm là:
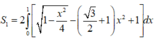
* Tính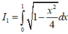 
. Đặt 
.
Đổi cận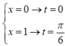 
Suy ra
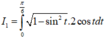
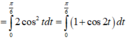
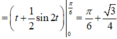
* Tính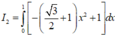 
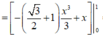
= 3 6 + 2 3
Vậy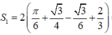 
= π 3 + 3 6 + 4 3 m2
Tổng số tiền sử dụng là:
≈ 2 . 341 . 000 đồng
Chọn đáp án A.
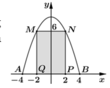
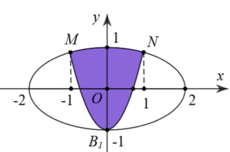
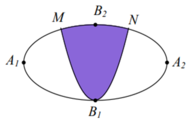
Chọn hệ trục tọa độ Oxy như hình vẽ.
Parabol đối xứng qua Oy nên có dạng 
Vì (P) đi qua B(4;0) và N(2;6) nên 
Diện tích hình phẳng giới hạn bởi (P) và trục Ox là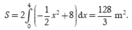
Diện tích phần trồng hoa là 
Do đó số tiền cần dùng để mua hoa là 
Chọn D.
Phương pháp:
+ Tìm phương trình Parabol
+ Diện tích hình phẳng giới hạn bởi
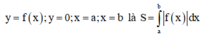
+ Tính diện tích hình chữ nhật từ đó tính diện tích phần trồng hoa và tính số tiền cần dùng để mua hoa trang trí.
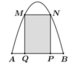
Cách giải:
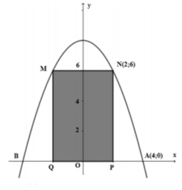
Gắn hệ trục tọa độ Oxy như hình vẽ, ta có Parabol đi qua các điểm A 4 ; 0 ; N 2 ; 6
Hoành độ giao điểm của Parabol và trục hoành là
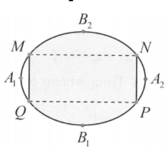
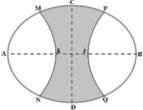
Chọn gốc toạ độ O=AB∩CD, các tia Ox, Oy lần lượt trùng với các tia OB, OC.
Elip có độ dài trục lớn AB=8m, độ dài trục nhỏ CD=6m có phương trình là
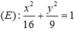
Diện tích của cả hình elip là 
Theo giả thiết có F(1;0) và
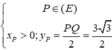
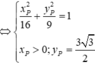
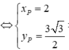
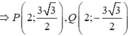
Parabol có trục đối xứng là Ox qua các điểm F, P, Q có dạng ( P ) : x = a y 2 + b y + c
Thay toạ độ các điểm F,P,Q vào phương trình parabol có
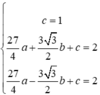
Nửa elip bên phải trục tung là
x
=
4
1
-
y
2
9
. Diện tích hình phẳng giới hạn bởi nửa elip này và parabol (P) là 
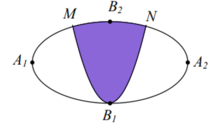
Diện tích phần tô đậm bằng
Số tiền cần dùng
≈ 4.809.142 đồng
Chọn đáp án D.
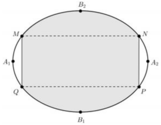
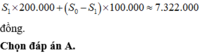
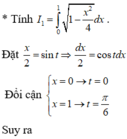
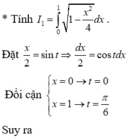
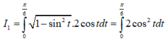
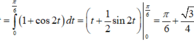
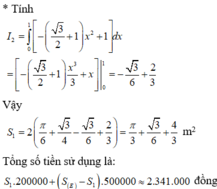
Đáp án là A