Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1h30' = 1,5h ; 2h42' = 2,7h
- Gọi x(phần bể) là phần bể tính từ đáy đến chỗ đặt vòi ra (x > 0)
--> phần bể tính từ chỗ đặt vòi ra đến miệng bể là : (1 - x) (phần bể)
- Vòi vào :
1,5h --> chảy đầy 1 bể
1h . --> chảy (1.1/1,5) = 2/3 bể
--> Vòi vào 1h chảy được 2/3 bể,vòi vào chảy mạnh gấp 2 lần vòi ra
--> Vòi ra 1h chảy ra được 1/3 bể
--> Tính từ lúc nước ngan chỗ đặt vòi chảy ra,mỗi h trong bể, nước sẽ có thêm:
(2/3 - 1/3) = 1/3 bể
- Thời gian để vòi 1 chảy từ đáy đến chỗ đặt vòi ra là : x : (2/3) = 3x/2(h)
- Cả 2 vòi cùng chảy,thời gian để nước chảy từ chỗ đặt vòi ra đến miệng bể là :
(1 - x) : 1/3 = 3(1 - x) (h)
- Tổng thời gian là 2,7h,nên ta có pt : 3x/2 + 3(1 - x) = 2,7
<=> 3x + 6(1 - x) = 5,4 <=> 3x = 0,6
<=> x = 0,2 = 1/5 (bể)
a) Thời gian nước chảy vào từ lúc bể cạn đến lúc nước ngan chỗ đặt vòi ra là :
3.0,2/2 = 0,3 (h) = 18'
b) Nếu chiều cao của bể là 2m thì khoảng cách từ chỗ đặt vòi chảy ra đến đáy là :
2.x = 2.0,2 = 0,4 (m)

Gọi thời gian chảy vào đầy bể là \(a\left(h\right)\left(a>0\right)\)
Gọi thời gian chảy ra hết bể là \(b\left(h\right)\left(b>0\right)\)
\(1h\)vòi chảy vào chảy được \(\frac{1}{a}\left(bể\right)\)
\(1h\)vòi chảy ra chảy được \(\frac{1}{b}\left(bể\right)\)
Ta có: \(\frac{1}{\frac{1}{a}-\frac{1}{b}}=6\Rightarrow\frac{1}{a}-\frac{1}{b}=\frac{1}{6}\left(h\right)\)
\(b-a=8\Rightarrow b=8+a\left(2\right)\)
Từ: \(\left(1\right)\left(2\right)\Rightarrow\frac{1}{a}-\frac{1}{a+8}=\frac{1}{6}\)
\(\Rightarrow\frac{a+8-a}{a\left(a+8\right)}=\frac{1}{6}\)
\(\Leftrightarrow a^2+8a=48\)
\(\Leftrightarrow a^2+8a-48=0\)
\(\Leftrightarrow a=4\)
Vậy ............

Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 0)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x+4) (bể)
- Vòi thứ ba chảy được 1/6 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
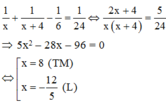
Vậy chỉ dùng vòi thứ nhất thì sau 8 giờ bể đầy nước
Đáp án: D

Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là x (giờ), (x > 2)
Trong một giờ:
- Vòi thứ nhất chảy được 1/x (bể)
- Vòi thứ hai chảy được 1/(x-2) (bể)
- Vì vòi thứ ba chảy ra trong 7,5 giờ thì cạn bể nên trong 1 giờ vòi thứ ba chảy được 2/15 (bể)
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước chảy ở bể ra nên ta có phương trình:

Vậy chỉ dùng vòi thứ nhất thì sau 10 giờ bể đầy nước
Đáp án: C

Gọi thời gian vòi 1 chảy một mình đẩy bể là x ( x<4)
Gọi thời gian vòi 2 chảy một mình đầy bể là y (y<4)
Trong một giờ:
-Vòi 1 chảy một mình được \(\dfrac{1}{x}\)(bể)
-Vòi 2 chảy được \(\dfrac{1}{y}\)(bể)
-Cả hai vòi chảy được \(\dfrac{1}{4}\)(bể)
+Ta có PT: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{9}\) (1)
Vì nếu để vòi 1 chảy một mình trong 30 phút rồi khóa lại và mở vòi hai trong 20 phút thì cả hai vòi chảy được 1/9 bể nên có PT:
\(\dfrac{1}{2}x+\dfrac{1}{3}y=\dfrac{1}{9}\)
⇔\(\dfrac{x}{2}+\dfrac{y}{3}=\dfrac{1}{9}\) (2)
Từ (1) và (2) ta có HPT: \(\left\{{}\begin{matrix}\dfrac{x}{1}+\dfrac{y}{1}=\dfrac{1}{4}\\\dfrac{x}{2}+\dfrac{y}{3}=\dfrac{1}{9}\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=6\\y=12\end{matrix}\right.\)(TM)
Vậy vòi 1 chảy một mình trong 6 giờ thì đẩy bể
Vậy vòi 2 chảy một mình trong 12 giờ thì đẩy bể

gọi 1/x là số nước chảy vào trong 1 h của vòi một
=> ... vòi hai là 1/X+6
ta có:
1/x+1/x+6 = 1/4
=> x bằng 6
. vậy nếu mở riêng từng vòi thì vòi 1 có thời gian là 6h
vòi hai là 10h