Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích tấm đồng hình vuông ở 0 ° C là S 0 = l 0 2 . Khi bị nung nóng, kích thước của tấm đồng tăng theo mọi hướng, nên diện tích của tấm đồng này ở t ° C sẽ là :
S = l 2 = l 0 + ∆ l 2 = l 0 2 + 2 l 0 ∆ l + ∆ l 2
Theo công thức nở dài : ∆ l = ∆ l 0 ∆ t.
Vì α = 17. 10 - 6 K - 1 khá nhỏ và ∆ t = t - t 0 = t không lớn, nên ∆ l << l 0
Do đó, bỏ qua ∆ l 2 và coi gần đúng.:
S ≈ S 0 + 2 l 0 ∆ l hay ∆ S = S - S 0 ≈ 2 α S 0 ∆ t
Từ đó suy ra :
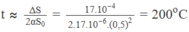

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l1 – ∆ l2 = l 01 α 1 t – l 02 α 2 t = ( l 01 α 1 – l 02 α 1 )t = 50 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t. Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
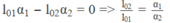
hay:
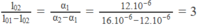
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 3( l 01 - l 02 ) = ∆ l = 3.50 = 150 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 150 + 50 = 200 mm.

Khi nhiệt độ tăng từ 0 ° C đến t ° C thì độ dãn dài của :
- Thanh thép : ∆ l 1 = l 01 α 1 t.
- Thanh đồng : ∆ l 2 = l 02 α 2 t.
Từ đó suy ra độ dài chênh lệch của hai thanh thép và đồng ở nhiệt độ bất kì t ° C có giá trị bằng :
∆ l = ∆ l 1 - l 2 l 1 = l 01 α 1 t - l 02 α 2 t = ( l 01 α 1 - l 02 α 2 )t = 25 mm
Công thức này chứng tỏ ∆ l phụ thuộc bậc nhất vào t.
Rõ ràng, muốn ∆ l không phụ thuộc t, thì hệ số của t phải luôn có giá trị bằng không, tức là :
l 01 α 1 - l 02 α 2 = 0 ⇒ l 02 / l 01 = α 1 / α 2
hay:
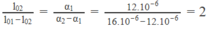
Từ đó suy ra độ dài ở 0 ° C của :
- Thanh đồng : l 02 = 2( l 01 - l 02 ) = ∆ l = 2.25 = 50 mm.
- Thanh thép : l 01 = l 02 + ∆ l = 50 + 25 = 75 mm.
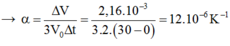
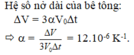
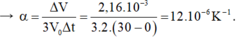

Đáp án: B
Độ tăng thể tích của bê tông: DV = 3aV0Dt