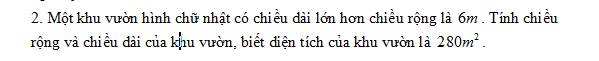Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, \(P=\frac{a^3-a+2b-\frac{b^2}{a}}{\left(1-\sqrt{\frac{a+b}{a^2}}\right)\left(a+\sqrt{a+b}\right)}:\left[\frac{a^2\left(a+b\right)+a\left(a+b\right)}{\left(a-b\right)\left(a+b\right)}+\frac{b}{a-b}\right]\)
\(=\frac{\frac{a^4-a^2-2ab-b^2}{a}}{\frac{\left(a-\sqrt{a+b}\right)\left(a+\sqrt{a+b}\right)}{a}}:\left[\frac{\left(a+b\right)\left(a^2+a\right)}{\left(a+b\right)\left(a-b\right)}+\frac{b}{a-b}\right]\)
\(=\frac{a^4-a^2-2ab-b^2}{a^2-a-b}:\frac{a^2+a+b}{a-b}\)
\(=\frac{a^4-a^2-2ab-b^2}{a^2-\left(a+b\right)}.\frac{a-b}{a^2+\left(a+b\right)}\)
\(=\frac{\left(a^4-a^2-2ab-b^2\right).\left(a-b\right)}{a^4-\left(a+b\right)^2}=\frac{\left[a^4-\left(a+b\right)^2\right].\left(a-b\right)}{a^4-\left(a+b\right)^2}=a-b\)
b, Có \(P=a-b=1\)\(\Rightarrow a=1+b\)
\(a^3-b^3=7\Leftrightarrow\left(a^2+ab+b^2\right)\left(a-b\right)=7\)
\(\Rightarrow a^2+ab+b^2=7\)
\(\Leftrightarrow\left(1+b\right)^2+\left(1+b\right)b+b^2=7\)
\(\Leftrightarrow b^2+2b+1+b^2+b+b^2=7\)
\(\Leftrightarrow3b^2+3b-6=0\)
Bạn tự giải phương trình tìm b => a
Bài 2 :
\(a,y=\left(m+1\right)x-2m-5\) \(\Leftrightarrow\left(m+1\right)x-2m-5-y=0\)
\(\Leftrightarrow mx+x-2m-5-y=0\)\(\Leftrightarrow m\left(x-2\right)+x-y-5=0\)
Có y luôn qua điểm A cố định với A( x0 ; y0 ) \(\orbr{\begin{cases}x_0-2=0\\x_0-y_0-5=0\end{cases}}\Rightarrow\orbr{\begin{cases}x_0=2\\y_0=-3\end{cases}}\)
=> A( 2;-3)
Gọi H là chân đường vuông góc hạ từ O xuống d => \(OH\le OA\)
\(OH_{max}=OA\)khi \(H\equiv A\)\(\left(d\perp OA\right)\)
=> đường thẳng OA qua O( 0;0 ) và A( 2;-3 ) => \(y=-\frac{3}{2}x\)
\(\Rightarrow d\perp OA\)=> hệ số góc \(m.\) \(-\frac{3}{2}=-1\Rightarrow m=\frac{2}{3}\)
b, \(y=0\Rightarrow\left(m+1\right)x-2m-5=0\)\(\Rightarrow x=\frac{2m+5}{m+1}\)\(\Rightarrow A\left(\frac{2m+5}{m+1};0\right)\)
\(x=0\Rightarrow y=-2m-5\Rightarrow B\left(0;-2m-5\right)\)
\(\Rightarrow OA=\sqrt{\frac{2m+5}{m+1}};OB=\sqrt{-2m-5}\)
\(\Rightarrow\frac{1}{2}.OA.OB=\frac{3}{2}\Rightarrow OA.OB=3\)
\(\Rightarrow\left(OA.OB\right)^2=9\Rightarrow\frac{\left(2m+5\right)^2}{m+1}=9\)
\(\Rightarrow4m^2+20m+25-9m-9=\)
\(\Rightarrow4m^2+11m+16=0\)

Gọi a (m) là chiều dài khu vườn, vậy chiều rộng là a-6 (m)
Diện tích khu vườn là a. (a-6) (m2)
Vì khu vườn có diện tích 280m2 nên ta có pt:
a. (a-6)= 280
<=> a2 - 6a - 280 = 0
<=> a2 - 20a + 14a - 280 =0
<=> a.(a-20) + 14. (a-20)= 0
<=> (a+14) . (a-20)=0
<=> a+14=0 hoặc a-20=0
<=> a= -14 (loại) hoặc a=20(nhận)
Vậy: Khu vườn có chiều dài là 20m, chiều rộng là 14m
Gọi x (m) là chiều rộng của khu vườn (x > 0)
Chiều dài của khu vườn là x + 6 (m)
Theo đề bài ta có phương trình:
x.(x + 6) = 280
⇔ x² + 6x - 280 = 0
∆´ = 9 + 280 = 289 > 0
Phương trình có hai nghiệm phân biệt:
x₁ = -3 + 17 = 14 (nhận)
x₂ = -3 - 17 = -20 (loại)
Vậy chiều rộng khu vườn là 14 m
Chiều dài khu vườn là 14 + 6 = 20 (m)




 mong mọi người làm nhanh giúp mình
mong mọi người làm nhanh giúp mình Mọi người giúp e làm câu 4c và bài 5 ạ
Mọi người giúp e làm câu 4c và bài 5 ạ