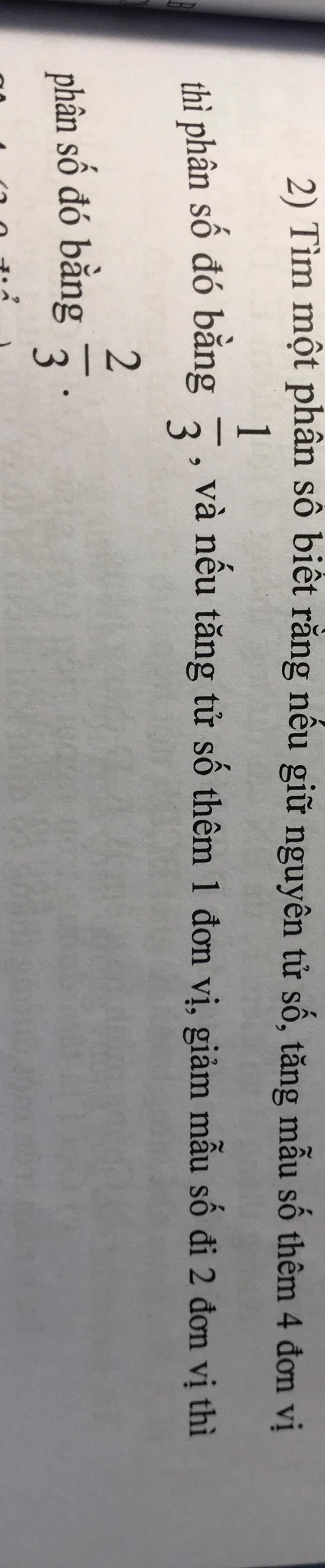Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


36B
37C
38D
39B
40D
41A
42B
43B
44A
45B
46B
47A
48C
50B
51B
52B
53D
54C
55D
56C


ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm

Câu 2:
1: \(y=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)x+4=\sqrt{3}+5\)
=>\(\left(\sqrt{3}-1\right)\cdot x=\sqrt{3}+5-4=\sqrt{3}+1\)
=>\(x=\dfrac{\sqrt{3}+1}{\sqrt{3}-1}=\dfrac{\left(\sqrt{3}+1\right)^2}{3-1}=\dfrac{4+2\sqrt{3}}{2}=2+\sqrt{3}\)
2: \(x^2-2\left(1-m\right)x-2m-5=0\)
=>\(x^2+\left(2m-2\right)x-2m-5=0\)
a: \(\Delta=\left(2m-2\right)^2-4\left(-2m-5\right)\)
\(=4m^2-8m+4+8m+20\)
\(=4m^2+24>=24>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
Câu 1:
2: Thay x=2 và y=-1 vào hệ phương trình, ta được:
\(\left\{{}\begin{matrix}2a-\left(-1\right)=5\\b\cdot2+a\cdot\left(-1\right)=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a=5+\left(-1\right)=4\\2b-a=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\2b=a+4=6\end{matrix}\right.\)
=>a=2 và b=3
2: Gọi phân số cần tìm có dạng là \(\dfrac{a}{b}\left(b\ne0\right)\)
Khi tăng mẫu số thêm 4 đơn vị thì phân số đó bằng 1/3 nên ta có:
\(\dfrac{a}{b+4}=\dfrac{1}{3}\)
=>3a=b+4
=>3a-b=4(1)
Khi giảm mẫu số đi 2 đơn vị thì phân số bằng với 2/3 nên ta có:
\(\dfrac{a}{b-2}=\dfrac{2}{3}\)
=>3a=2(b-2)
=>3a=2b-4
=>3a-2b=-4(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a-b=4\\3a-2b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=8\\3a-b=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=8\\3a=b+4=12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=8\end{matrix}\right.\)(nhận)
Vậy: Phân số cần tìm là \(\dfrac{4}{8}\)

Bài 3:
\(a,ĐK:2\le x\le1+\sqrt{5}\\ PT\Leftrightarrow4+2x-x^2=x^2-4x+4\\ \Leftrightarrow2x^2-6x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=3\left(tm\right)\end{matrix}\right.\\ \Leftrightarrow x=3\\ b,ĐK:1\le x\le5\\ PT\Leftrightarrow25-x^2=x^2-2x+1\\ \Leftrightarrow2x^2-2x-24=0\\ \Leftrightarrow\left(x+3\right)\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-3\left(ktm\right)\\x=4\left(tm\right)\end{matrix}\right.\Leftrightarrow x=4\\ c,PT\Leftrightarrow3x^2-9x+1=x^2-4x+4\\ \Leftrightarrow2x^2-5x-3=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-\dfrac{1}{2}\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=3\)

a) Xét (O) có
\(\widehat{BAD}\) là góc nội tiếp chắn \(\stackrel\frown{BD}\)
\(\widehat{CAD}\) là góc nội tiếp chắn \(\stackrel\frown{CD}\)
mà \(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
nên \(\stackrel\frown{BD}=\stackrel\frown{CD}\)
hay BD=CD
Ta có: OB=OC(=R)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: BD=CD(cmt)
nên D nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OD là đường trung trực của BC
hay OD\(\perp\)BC(đpcm)

a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OM là đường trung trực của AB
hay OM\(\perp\)AB
b: Xét ΔMAD và ΔMCA có
\(\widehat{MAD}=\widehat{MCA}\)
\(\widehat{AMD}\) chung
Do đó: ΔMAD\(\sim\)ΔMCA
Suy ra: MA/MC=MD/MA
hay \(MA^2=MC\cdot MD\)