YM
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
J
2
26 tháng 12 2018
Đoạn mạch nối tiếp
I=I1=I2 , U=U1+U2 , R=R1+R2
Đoạn mạch song song
I=I1+I2 , U=U1=U2 , \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}\Rightarrow R_{tđ}=\dfrac{R_1\times R_2}{R_1+R_2}\)
29 tháng 12 2018
* Trong đoạn mạch nối tiếp :
+ Cường độ dòng điện:
\(I_{AB}=I_1=I_2=...=I_n\)
+ Hiệu điện thế :
\(U_{AB}=U_1+U_2+...+U_n\)
+ Điện trở :
\(R_{AB}=R_1+R_2+...+R_n\)
*Trong đoạn mạch song song
+ Cường độ dòng điện:
\(I_{AB}=I_1+I_2+...+I_n\)
+ Hiệu điện thế :
\(U_{AB}=U_1+U_2+...+U_n\)
+ Điện trở :
\(\dfrac{1}{R_{AB}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+...+\dfrac{1}{R_n}\)
VT
21 tháng 11 2018
Đáp án D
Giữa I 1 , I 2 , I 3 có mối liên hệ là I 2 = I 3 = I 1 / 2
VT
12 tháng 4 2017
R1 và R2 mắc nối tiếp nên dòng điện chạy qua chúng có cùng cường độ I.
Kí hiệu nhiệt lượng tỏa ra ở các điện trở này tương ứng là Q1 và Q2
Ta có: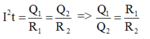 
→ Đáp án A
8 tháng 11 2023
\(R_1//R_2\Rightarrow R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}\)
\(I=I_1+I_2\)
Chọn C.
23 tháng 8 2021
R1 nt R2\(=>I1=I2=>I1^2=I2^2\)
\(=>\dfrac{Q1}{Q2}=\dfrac{I1^2R1t}{I2^2R2t}=\dfrac{R1}{R2}\left(đpcm\right)\)
b,R1//R2\(=>U1=U2=>U1^2=U2^2\)
\(=>\dfrac{Q1}{Q2}=\dfrac{I1^2R1t}{I2^2R2t}=\dfrac{\dfrac{U1^2}{R1}}{\dfrac{U2^2}{R2}}=\dfrac{R2}{R1}\left(dpcm\right)\)
K
23 tháng 8 2021
Có hai điện trở R1 = 120Ω và R2 = 80Ω được mắc nối tiếp vào mạch điện có hiệu điện thế 220V trong thời gian 1 giờ.
a,Tính nhiệt lượng toả ra trên mỗi điện trở trong thời gian đó
b, Tính nhiệt lượng toả ra trên toàn mạch và so sánh với nhiệt lượng toả ra trên hai điện trở đó.
Giải giúp mik đi
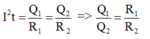
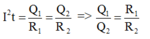
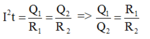
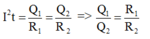
* Trong đoạn mạch nối tiếp :
+ Cường độ dòng điện:
IAB=I1=I2=...=InIAB=I1=I2=...=In
+ Hiệu điện thế :
UAB=U1+U2+...+UnUAB=U1+U2+...+Un
+ Điện trở :
RAB=R1+R2+...+RnRAB=R1+R2+...+Rn
*Trong đoạn mạch song song
+ Cường độ dòng điện:
IAB=I1+I2+...+InIAB=I1+I2+...+In
+ Hiệu điện thế :
UAB=U1+U2+...+UnUAB=U1+U2+...+Un
+ Điện trở :
Nối tiếp:
\(\left\{{}\begin{matrix}R=R1+R2+...+Rn\\I=I1=I2=..=In\\U=U1=U2=...=Un\end{matrix}\right.\)
Song song:
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}R=\dfrac{R1.R2}{R1+R2}\\\dfrac{1}{R}=\dfrac{1}{R1}+\dfrac{1}{R2}+...\dfrac{1}{Rn}\end{matrix}\right.\\I=I1+I2+...+In\\U=U1=U2=...Un\end{matrix}\right.\)