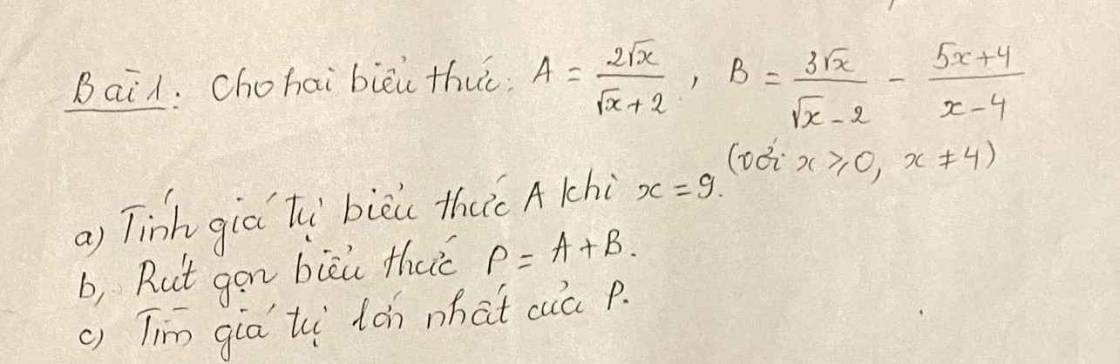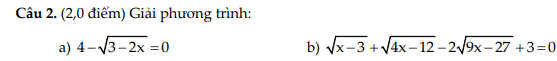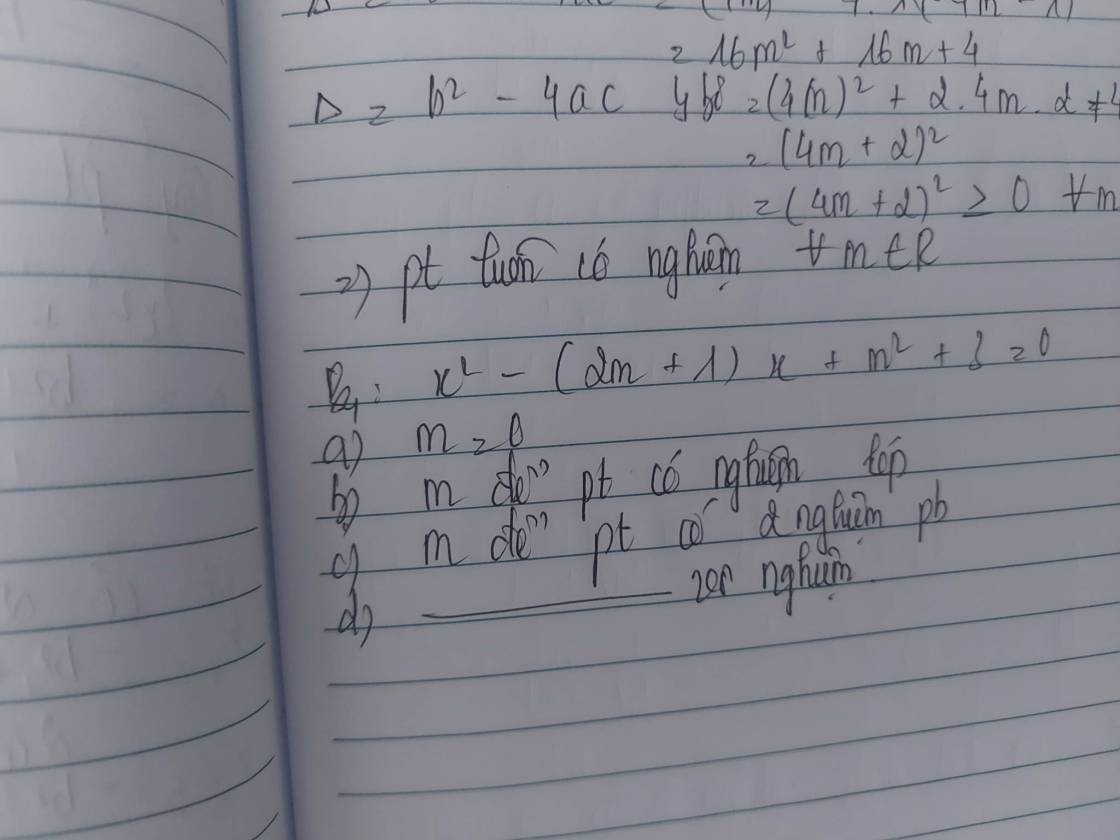Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phần trắc nghiệm:
Hàm số bậc nhất biến $x$ có dạng $y=ax+b$ với $a, b\in\mathbb{R}, a\neq 0$.
1. A
2. C
3. A
4. B
5. B
6. A
7. B
8. C


a.
Khi \(x=9\Rightarrow A=\dfrac{2\sqrt{9}}{\sqrt{9}+2}=\dfrac{6}{5}\)
b.
\(P=\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{3\sqrt{x}}{\sqrt{x}-2}-\dfrac{5x+4}{x-4}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{3\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{5x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2x-4\sqrt{x}+3x+6\sqrt{x}-5x-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2}{\sqrt{x}+2}\)
c.
Do \(x\ge0\Rightarrow\sqrt{x}+2\ge2\)
\(\Rightarrow\dfrac{2}{\sqrt{x}+2}\le\dfrac{2}{2}=1\)
Vậy \(P_{max}=1\) khi \(x=0\)

d: Để (d1) vuông góc với y=(k-1)x+4 thì \(\left(k-1\right)\left(k-3\right)=-1\)
\(\Leftrightarrow k=2\)

a: \(4-\sqrt{3-2x}=0\)
\(\Leftrightarrow3-2x=16\)
hay \(x=-\dfrac{13}{2}\)

a: góc BEC=góc BFC=90 độ
=>BFEC nội tiếp
góc AEH+góc AFH=180 độ
=>AEHF nội tiếp
b: góc ABT=1/2*180=90 độ
=>BT vuông góc AB
=>BT//CH
góc ACT=1/2*180=90 độ
=>AC vuông góc CT
=>CT//BH
mà BT//CH
nên BHCT là hình bình hành


`a)m=0=>x^2-x+3=0<=>(x-1/2)^2+11/4=0` (Vô lí)
`=>m=0` ptr vô nghiệm
`b)` Ptr có nghiệm kép `<=>\Delta=0`
`<=>[-(2m+1)]^2-4(m^2+3)=0`
`<=>4m^2+4m+1-4m^2-12=0`
`<=>4m-11=0`
`<=>m=11/4`
`c)` Ptr có `2` nghiệm pb`<=>\Delta > 0`
`<=>4m-11 > 0<=>m > 11/4`
`d)` Ptr vô nghiệm `<=>\Delta < 0<=>4m-11 < 0<=>m < 11/4`
Bài 2:
a: Khi m=0 thì pt sẽ là:
\(x^2-x+3=0\)
=>\(x\in\varnothing\)
b: \(\Delta=\left(2m+1\right)^2-4\left(m^2+3\right)\)
=4m^2+4m+1-4m^2-12
=4m-11
Để pt có nghiệm kép thì 4m-11=0
=>m=11/4
c: Để phương trình có hai nghiệm pb thì 4m-11>0
=>m>11/4
d: Để pt vô nghiệm thì 4m-11<0
=>m<11/4