Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(Q_{thu}=Q_{tỏa}\)
\(\Rightarrow36-t_1=t_2-36\)
\(\Rightarrow36-t_1=2t_1-36\) \(\Leftrightarrow t_1=24^oC\) \(\Rightarrow t_2=48^oC\)

Vì: Hai bình nước giống nhau, chứa cùng lượng nước, nên
Ta có:Pt cân bằng nhiệt:
Qtỏa=Qthu
<=>m.c.(t2-25)=m.c.(25-t1)
<=>t2-25=25-t1
<=>\(\dfrac{3}{2}t_1\)-25=25-t1
<=>t1=20oC
=>t2=\(\dfrac{3}{2}.20=30^oC\)

gọi Vn là thể tích nước chứa trong bình
Vb là thể tích của bi nhôm , klr của nước và nhom lần lượt là Dn , Db , ndr lần lượt là cn , cb
do bình chưa đầy nước nên khi thả viên bi vào lượng nước tràn ra có thể tích = thể tích của bi nhôm ( Vt ( V tràn ) = Vb)
ta có ptcbn lần 1
mbcb ( t-t1 ) = m'n.cn (t-t0 )
vs m'n là kl nước sau khi bị tràn
<=> db.vb .cb(t-t1) = (vn-vb ) dncn(t1-t0)
thay số ta đc : Vb (188190cb+ 43260000) = 43260000vn (1)
- khi thả thêm 1 viên bi nữa ta có ptcbn
(m'n.cn + mb.cb ) ( t2-t1 ) = mb.cb(t-t2 )
[(vn-2vb) dn.cn+db.vb.cb] (t2-t1 ) = db.vb.cb(t-t2)
thay số vào ta đc : vb ( 121770cb + 103320000) = 51660000vn (2)
lấy (1) : (2 ) ta có
vb(188190cb+43260000)/ vb(121770cb+103320000) = 43260000vn/ 51660000vn
=> cb = 501,7J/kg.k
Tại mình lm biến gõ công thức nên nhìn bài giả lộn xộn quá , xin mọi người thông cảm
nếu có sai xót thì chỉ giúp ạ !!!
Bài này lâu quá, mình quên cách làm rồi.
Bạn giải cho mọi người tham khảo nhé.

Đáp án: B
- Nhiệt lượng do xô và nước toả ra để hạ nhiệt độ xuống 0°C là:
![]()
- Nhiệt lượng thu vào của 1 viên nước đá để tăng nhiệt độ lên 0°C và tan hết tại 0°C là:
![]()
- Số viên nước đá cần phải thả vào nước là:
705000 : 83760 = 8,4
- Vậy phải thả vào xô ít nhất 9 viên đá để nhiệt độ cuối cùng trong xô là 0 0 C

Đáp án: D
- Khi thả hai viên nước đá vào chậu nước. Giả sử nước đá tan hết ở 0 0 C .
- Nhiệt lượng do chậu và nước toả ra để hạ nhiệt độ xuống 0 0 C là:
Q 1 = ( m c + m 1 c 1 ) ( t 1 - 0 ) = 47000 ( J )
- Nhiệt lượng thu vào của 2 viên nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
Q 2 = 2 m 2 C 2 ( 0 - t 2 ) + 2 m 2 . λ = 13960 ( J )
- Vì Q 1 > Q 2 nên 2 viên đá sẽ tan hết và nhiệt độ cân bằng 0 0 C < t < 20 0 C .

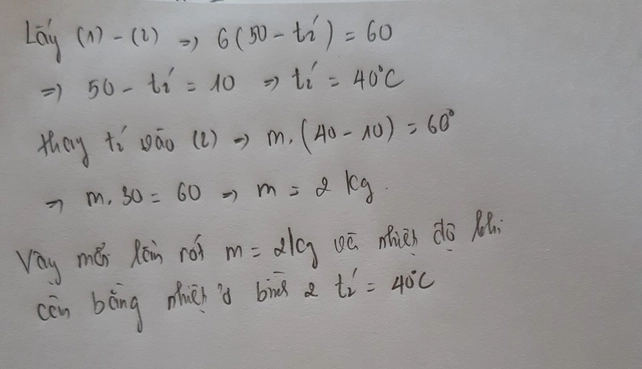 Đây là bài làm tương tự nhé!
Đây là bài làm tương tự nhé!
Mình trình bày hơi tắc nên chỗ nào ko hiểu bạn có thể ib hỏi minh nha!
Gọi \(Q_2,Q_3,Q_4\) lần lượt là nhiệt lượng thu vào của nước ở mỗi đợt thả bi
\(Q_1\) lần lượt là nhiệt lượng tỏa ra của viên bi
m và c lần lượt là khối lượng và nhiệt dung của bình nước
\(m_1vàc_1\) lần lượt là khối lượng và nhiệt dung của viên bi
Phương trình cân bằng lần 1:\(Q_1=Q_2\Rightarrow m_1c_1\left(t_2-33,2\right)=mc\left(33.2-t_1\right)\)(1)
Phương trình cân bằng lần 2:\(Q_1=Q_3\Rightarrow m_1c_1\left(t_2-44\right)=mc\left(44-33,2\right)\Leftrightarrow m_1c_1\left(t_2-44\right)=mc\cdot10,8\)(2)
Phương trình cân bằng lần 3:
\(Q_1=Q_4\Rightarrow m_1c_1\left(t_2-53\right)=mc\left(53-44\right)\Leftrightarrow m_1c_1\left(t_2-53\right)=mc\cdot9\)(3)
ta lấy (2) chia(3) được phương trình mới là:
\(\dfrac{t_2-44}{t_2-53}=\dfrac{10,8}{9}\Rightarrow t_2=98^oC\)
ta lấy (1) chia (2) dc phương trình mới là:
\(\dfrac{t_2-33,2}{t_2-44}=\dfrac{33,2-t_1}{10,8}\)
thay t2 =98 vào pt trên ta dc
\(\dfrac{98-33,2}{98-44}=\dfrac{33,2-t_1}{10,8}\Rightarrow t_1=20,24^oC\)
vậy \(t_1=20,24^oC;t_2=98^oC\)