Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Tần số góc: \(\omega=\sqrt{\dfrac{k}{m}}=\sqrt{\dfrac{100}{0,1}}=10\pi(rad/s)\)
Biểu diễn dao động bằng véc tơ quay, tại thời điểm 7/60s thì véc tơ quay đã quay 1 góc là: \(\alpha=\omega.t=\dfrac{7}{6}\pi\)
Tại vị trí \(W_đ=3.W_t\)\(\Rightarrow W=W_đ+W_t=4W_t\)
\(\Rightarrow x=\pm\dfrac{A}{2}=\pm 2cm\)
x 4 -4 2 -2 M N O
Vì tốc độ của vật đang giảm nên có 2 trường hợp:
+ TH1: Dao động ứng với trạng thái tại M, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên âm --> Li độ là -4cm.
+ TH2: Dao động ứng với trạng thái N, sau khi quay \(\dfrac{7}{6}\pi\) sẽ đến biên độ dương -> Li độ là 4cm.

1. Biểu diễn bằng véc tơ quay, trong thời gian T/6 thì véc tơ quay góc: 360/6 = 600
Vật đạt tốc độ cực đại khi nó đi qua VTCB, ta có:
M N O 30 30 A/2 -A/2 A -A
Như vậy, quãng đường vật đi trong T/6 là: A/2 + A/2 = A.
Tốc độ trung bình cực đại: \(v=\frac{S}{t}=\frac{A}{\frac{T}{6}}=6\frac{A\omega}{2\pi}=\frac{3.A.4\pi}{2\pi}=60\)\(\Rightarrow A=10\)cm
2. Biên độ A = 10/2 = 5cm.
Khi vật có Wd = 0,009 J thì thế năng: \(W_t=W-W_đ=\frac{1}{2}.20.0,05^2-0,009=0,016\)J
Suy ra: \(\frac{1}{2}.20.x^2=0,016\Rightarrow x=4\)cm

Chọn A
Tại thời điểm cố định lò xo ta có E d = n E t E d + E t = E → E t = E n + 1 E d = n E n + 1
+ Vì thế năng đàn hồi của lò xo phân bố đều trên mỗi đơn vị chiều dài, do vậy thế năng của hệ dao động mới là E ' t = E t m = E m n + 1
+ Cơ năng của hệ dao động mới: E ' = E ' t + E ' d = E m n + 1 + n E n + 1 = 1 2 k ' A ' 2
Trong đó k′ = mk là độ cứng của phần lò xo tham gia vào dao động của vật lúc sau.
→ Biến đổi toán học ta thu được tỉ số A ' A = m n + 1 2 m n + 1

1) \(W_đ=W_t\Rightarrow W=W_đ+W_t=2W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=2.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{A}{\sqrt 2}\)
Như vậy, trong 1 chu kì có 4 lần động năng bằng thế năng được biểu diễn bằng véc tơ quay như sau.
x A -A O M N P Q
Đó là các vị trí ứng với véc tơ quay đi qua M, N, P, Q
Như vậy, thời gian giữa 2 lần liên tiếp động năng bằng thế năng là 1/4T
\(\Rightarrow \dfrac{T}{4}=0,2\Rightarrow T = 0,8s\)
\(W_đ=nW_t\)
\(\Rightarrow W = W_đ+W_t=nW_t+W_t=(n+1)W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=(n+1).\dfrac{1}{2}kx^2\)
\(\Rightarrow \dfrac{A}{x}=\pm\sqrt{n+1}\)
\(\Rightarrow \dfrac{\omega^2. A}{-\omega^2.x}=\pm\sqrt{n+1}\)
\(\Rightarrow \dfrac{a_{max}}{a}=\pm\sqrt{n+1}\)

13. Một con lắc lò xo dao động với biên độ 5cm. Xác định li độ của vật để thế năng của vật bằng động năng của nó.
Li độ của vật để thế năng của vật bằng động năng của nó
\(\left\{{}\begin{matrix}W_d=W_t\\W_d+W_t=W\end{matrix}\right.\)=> \(W_t=\dfrac{W}{2}\)
\(\dfrac{1}{2}kx^2=\dfrac{1}{2}.\dfrac{1}{2}kA^2\)
\(\Rightarrow x=\pm\dfrac{A}{\sqrt{2}}\)
12. Một con lắc lò xo dao động với biên độ 10cm. Xác định li độ của vật để thế năng của vật bằng 3 động năng của nó.
\(W=W_d+W_t\)
\(\Leftrightarrow\dfrac{1}{2}kA^2=3W_t+W_t\)
\(\Leftrightarrow\dfrac{1}{2}kA^2=4W_t=4\dfrac{1}{2}kx^2\)
\(\Rightarrow x=\pm\dfrac{A}{2}\)

Chọn A
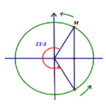
+ E = 1 2 kA2 = 0,5J (nhớ đổi đơn vị của A).
+ Chất điểm ở M nhận cùng một li độ và ngược chiều nhau,ta có hình minh họa. Từ hình vẽ => x = ± A/2.
+ Wđ = 3Wt
(dùng công thức Wđ = nWt ⇔ x = ± A n + 1 )
=> Wđ = 3 4 E = 0,375J = 375mJ.

Khoảng thời gian ngắn nhất giữa hai lần liên tiếp vật vật đi qua vị trí có li độ
![]()
+ Lực kéo cực đại của lò xo tác dụng và điểm có định là
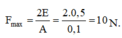
+ Vậy khoảng thời gian ngắn nhất để lò xo kéo điểm cố định một lực 5 N là
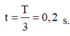
Đáp án D