K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
mọi người giải giúp em ý 2 vs ạ. Em cảm ơn nhiều
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 1 2022
\(\Rightarrow\sqrt{2x^2+2x+3}-\sqrt{2x^2-1}+\sqrt{x^2-x+2}-\sqrt{x^2-3x-2}=0\)
\(\Leftrightarrow\dfrac{2x+4}{\sqrt{2x^2+2x+3}+\sqrt{2x^2-1}}+\dfrac{2x+4}{\sqrt{x^2-x+2}+\sqrt{x^2-3x-2}}=0\)
\(\Leftrightarrow\left(x+2\right)\left(\dfrac{2}{\sqrt{2x^2+2x+3}+\sqrt{2x^2-1}}+\dfrac{2}{\sqrt{x^2-x+2}+\sqrt{x^2-3x-2}}\right)=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\)
Thứ lại nghiệm thấy thỏa mãn (do ban đầu ko tìm ĐKXĐ nên cần thử lại). Vậy \(x=-2\) là nghiệm duy nhất của pt
19 tháng 1 2023
Câu 5:
ABCD là hình bình hành
=>vecto AB=vecto DC
=>\(\left\{{}\begin{matrix}4-x=2-0=2\\-1-y=1+3=4\end{matrix}\right.\Leftrightarrow D\left(2;-5\right)\)
Câu 6:
vecto c=k*vecto a+m*vecto b
=>\(\left\{{}\begin{matrix}-1=2k+3m\\7=-3k+m\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k=-2\\m=1\end{matrix}\right.\)
=>k+m=-1
Câu 7: B
Câu 8: C
6 tháng 9 2021
Đặt y = f(x) = - 2x2 có đồ thị (C)
và y = g(x) = - 2x2 - 6x + 3 có đồ thị (C')
Ta có :
g(x) = - 2x2 - 6x + 3
= - 2\(\left(x^2+3x-\dfrac{3}{2}\right)\)
= - 2\(\left(x+\dfrac{3}{2}\right)^2\) + \(\dfrac{15}{2}\)
= \(f\left(x+\dfrac{3}{2}\right)+\dfrac{15}{2}\)
Vậy tịnh tiến (C) sang trái \(\dfrac{3}{2}\) đơn vị rồi kéo (C) lên trên \(\dfrac{15}{4}\) đơn vị ta được (C')
SN
1
1 tháng 4 2022
Câu 2:
\(TH1:m+2=0. \Leftrightarrow m=-2.\)
Thay \(m=-2\) vào BPT ta có:
\(0x+\left(-2\right)^2-3>0.\\ \Leftrightarrow4-3>0.\)
\(\Leftrightarrow1>0\) (Luôn đúng).
Vậy \(m=-2\) thì BPT có nghiệm.
\(TH2:m+2\ne0.\Leftrightarrow m\ne-2.\)
Khi đó BPT có nghiệm \(x>\dfrac{3-m^2}{m+2}.\)
Vậy bất phương trình có nghiệm với mọi giá trị thực của m.
TC
2
KH
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 5 2021
Từ pt (E) ta xác định được: \(a=5;b=3;c=4\)
\(F_1F_2=2c=8\Rightarrow\) chu vi tam giác \(MF_1F_2=MF_1+MF_2+F_1F_2=2a+2c=18\)
\(\Rightarrow\) nửa chu vi \(p=9\)
Tam giác \(MF_1F_2\) vuông tại M \(\Rightarrow OM=\dfrac{1}{2}F_1F_2=4\)
Gọi \(M\left(x;y\right)\Rightarrow\overrightarrow{OM}=\left(x;y\right)\Rightarrow OM^2=x^2+y^2=16\)
\(\Rightarrow x^2=16-y^2\)
Thay vào pt (E):
\(\dfrac{16-y^2}{25}+\dfrac{y^2}{9}=1\Rightarrow y^2=\dfrac{81}{16}\Rightarrow\left|y\right|=\dfrac{9}{4}\)
\(S_{MF_1F_2}=\dfrac{1}{2}F_1F_2.d\left(M;F_1F_2\right)=\dfrac{1}{2}.2c.\left|y\right|=9\)
\(\Rightarrow r=\dfrac{S_{MF_1F_2}}{p}=1\)
HP
20 tháng 5 2021
13.
\(\dfrac{sinx-sin3x+sin5x}{cosx-cos3x+cos5x}\)
\(=\dfrac{2sin3x.cos2x-sin3x}{2cos3x.cos2x-cos3x}\)
\(=\dfrac{\left(2cos2x-1\right)sin3x}{\left(2cos2x-1\right)cos3x}\)
\(=\dfrac{sin3x}{cos3x}=tan3x\)
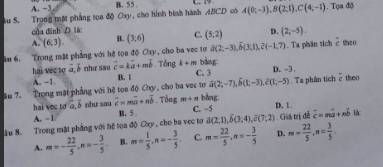
1. \(\dfrac{4x}{4x^2-8x+7}+\dfrac{3x}{4x^2-10x+7}=1\)
Dễ thấy \(x=0\) ko phải là nghiệm của pt
Chia tử và mẫu cho x, ta được:
\(\dfrac{4}{4x-8+\dfrac{7}{x}}+\dfrac{3}{4x-10+\dfrac{7}{x}}=1\) (*)
Đặt \(t=4x+\dfrac{7}{x}-8\) thì:
(*) \(\Rightarrow\dfrac{4}{t}+\dfrac{3}{t-2}=1\)
Quy đồng lên tìm được t, sau đó dễ dàng tìm được x.
2 bài kia tương tự bạn nhé, cũng chia tử và mẫu cho x rồi đặt ẩn phụ
Bài 2 đặt \(t=x+\dfrac{15}{x}\)
Bài 3 đặt \(t=x+\dfrac{3}{x}\)