Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = 350/0,005= 0,7. 10 5 Pa; p = 1,7.105 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3
n’ = 2n = 19 lần.

Thể tích của bơm:
V = s . h = π d 2 4 . h = 3 , 14. h 2 4 .50
= 981 , 25 c m 3
Gọi n là số lần bơm để không khí đưa vào săm có áp suất p 1 và thể tích V 1 .
Ta có: p = p 1 + p 0 hay
p 1 = p − p o = ( 5 − 1 ) 10 5 = 4.10 5 N / m 2 .
Theo định luật Bôi-lơ – Ma-ri-ốt:
n p o V o = p 1 V 1 hay
n = p 1 V 1 p o V o = 4.10 5 .7.10 3 10 5 .981 , 25 ≈ 29 lần.
Cứ 1 lần bơm mất thời gian là 2,5s
⇒ 29 lần bơm mất thời gian là t = 72,5s

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p 0 + p’
Với p’ = F/S = 350/0,005 = 0,7. 10 5 Pa;
→ p = 1,7. 10 5 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3 .
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n c m 3 không khí được đưa vào bánh. Ban đầu có 1500 c m 3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa; V2 = 2000 c m 3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p 0 + p’
Với p’ = F/S = 350/0,005 = 0,7. 10 5 Pa;
→ p = 1,7. 10 5 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3 .
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n cm3 không khí được đưa vào bánh. Ban đầu có 1500 cm3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V 1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa; V 2 = 2000 cm3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Đáp án: C
Ta có:
Thể tích khí bơm được sau 20 lần bơm là 20.0,125 lít
+ Thể tích của không khí trước khi bơm vào bóng: V 1 = 20.0,125 + 2,5 = 5 l (Bao gồm thể tích khí của 20 lần bơm và thể tích khí của khí có sẵn trong bóng)
+ Sau khi bơm khí vào trong bóng thể tích lượng khí chính bằng thể tích của bóng: V 2 = 2,5 l
Do nhiệt đọ không đổi, theo định luật Bôi lơ – Ma ri ốt, ta có:
p 1 V 1 = p 2 V 2 ⇔ 10 5 .5 = p 2 .2,5 ⇒ p 2 = 2.10 5 P a

Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = 350/0,005= 0,7. 10 5 Pa; p = 1,7.105 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n c m 3 không khí được đưa vào bánh. Ban đầu có 1500 c m 3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V 1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa ; V 2 = 2000 c m 3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần.

Đáp án A.
p 1 V 1 = p 2 V 2 ⇒ 10 5 0 , 125.20.2 , 5 = p 2 .2 , 5 ⇒ p 2 = 2.10 5 P a

Đáp án C
Xét khối khí trong bóng sau 12 lần bơm. Trước khi bơm vào bóng, khối khí đó có thể tích là: V0=12.0,125+2,5=4 l và áp suất của khối khí đó ban đầu là P0 = 1atm. Sau khi bơm vào bóng thể tích của khối khí đó là V = 2,5l và áp suất của quá trình đó là P
Vì nhiệt độ là không đổi trong suốt quá trình bơm, do đó áp dụng định luật Bôi-lơ-ma-ri-ốt, ta có:
![]()
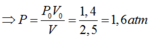
thể tích mỗi lần bơm
V=0,08lít
\(TT_1\left\{{}\begin{matrix}V_1=n.V\\p_1=10^5Pa\end{matrix}\right.\) (n là số lần bơm)
\(TT_2\left\{{}\begin{matrix}p_2=2.10^5Pa\\V_2=2000cm^3=2lít\end{matrix}\right.\)
đẳng nhiệt
\(p_1.V_1=p_2.V_2\)
\(\Rightarrow n=\)50 lần