Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Kết quả ra số thập phân, nếu không đúng thì do đề bài sai*
Giải :
Mỗi bao xi cân nặng :
1260 : 24 = 52,5 ( kg )
27 bao xi cân nặng :
52,5 x 27 = 1417,5 ( kg )
31 bao xi cân nặng :
52,5 x 31 = 1627,5 ( kg )
Cả 3 xe cân nặng :
1260 + 1417,5 + 1627,5 = 4305 ( kg ) = 43,05 tạ
Đáp số :......
bài này tính 1 bao là lấy 1260:24 rồi tìm các bao 27 và 31 xong cộng lại rồi đổi là ra kết quả nha!

Hiệu hai kho là:
70,8 - 48,6 =22,2
Hiệu số phần là
5-2=3
Giá trị 1 phần là ;
22,2 : 3 = 7,4
Kho thứ hai sau khi lấy là
7,4 x 2 = 14,8
Kho thứ nhất sau khi lấy là
7,4 nhân 5 =37
Số tấn gạo lấy đi ở kho thứ hai là
48,6 - 14,8 =33.8
Vậy kho thứ 1 cũng sẽ bị lấy ra 33.8 tấn gạo
Đáp số ; 33.8

Gọi số gạo lúc đầu của kho A là a ( tấn ), kho B là b ( tấn )
Lần đầu chuyển kho A còn lại: \(a-4+\left(a-4\right).3=\left(a-4\right).4\)
Lần đầu chuyển kho B còn lại: \(b+4-\left(a-4\right).3\)
Tương tự:
Lần thứ 2 chuyển kho A còn lại: \(\left(a-4-4\right).4=\left(a-8\right).4\)
Lần thứ 2 chuyển kho B còn lại: \(b+4+4-\left(a-4-4\right).3=b+8-\left(a-8\right).3\)
Lần thứ 3 chuyển kho A còn lại: \(\left(a-8-4\right)=\left(a-12\right).4\)
Lần thứ 3 chuyển kho B còn lại: \(b+8+4-\left(a-8-4\right).3=b+12-\left(a-12\right).3\)
Ta có: \(\left(a-12\right).4=48\)0
\(a-12=120\)
=> a = 132
\(b+12-\left(a-12\right).3=20\)
=> \(b+12-\left(240-12\right).3=20\)
=> \(b+12-228.3\) = 20
=> b = 692
Vậy............

Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
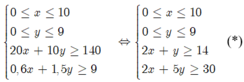
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

Lời giải:
Buổi chiều cửa hàng bán được số kg gạo là:
\(75.60\text{%}=75.\frac{60}{100}=45\)(kg)
Cả hai buổi bán được : \(75+45=120\) (kg) \(=1,2\) (tạ gạo)

mình nghĩ bài này còn thiếu dữ kiện nữa thì mới có thể làm đc bn ạ
Đổi: 9 tấn =90 tạ
Số bao ô tô chở được: \(90:3=30\left(bao\right)\)
=> Chọn C
Chọn C