K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 2 2023
a: Xét ΔABM vuông tại M và ΔACN vuông tại N có
góc BAM chung
=>ΔABM đồng dạng với ΔACN
b: ΔABM đồng dạng với ΔACN
=>AM/AN=AB/AC
=>AM/AB=AN/AC
mà góc MAN chung
nen ΔAMN đồng dạng với ΔABC
c: Xét ΔBKH vuông tại K và ΔBMC vuông tại M có
góc KBH chung
=>ΔBKH đồng dạng với ΔBMC
=>BK/BM=BH/BC
=>BK*BC=BH*BM
Xét ΔCKH vuông tại K và ΔCNB vuông tại N có
góc KCH chung
=>ΔCKH đồng dạng với ΔCNB
=>CK/CN=CH/CB
=>CK*CB=CH*CN
=>BH*BM+CH*CN=BK*BC+CK*BC=BC^2
d: ΔANM đồng dạng với ΔABC
=>\(\dfrac{S_{ANM}}{S_{ABC}}=\left(\dfrac{AN}{AB}\right)^2=\dfrac{1}{4}\)
=>ĐPCM
19 tháng 8 2023
2:
1: =7x(x-y)-5(x-y)
=(x-y)(7x-5)
2: =(x^2-y^2)-(4x-4y)
=(x-y)(x+y)-4(x-y)
=(x-y)(x+y-4)
3: =(x^2+2xy+y^2)-(2x+2y)+1
=(x+y)^2-2(x+y)+1
=(x+y-1)^2
5 tháng 4 2022
a: \(\Leftrightarrow2x\left(x+2\right)+4>x^2+4x+4\)
\(\Leftrightarrow2x^2+4x-x^2-4x>0\)
=>x<>0
b: \(\Leftrightarrow3\left(1-2x\right)-24x< 4\left(1-5x\right)\)
=>3-6x-24x<4-20x
=>-30x+3<4-20x
=>-10x<1
hay x>-1/10
c: \(\Leftrightarrow x^2+6x+8>x^2+10x+16+26\)
=>6x+8>10x+42
=>-4x>34
hay x<-17/2
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2022
Gọi khối lượng cá dự định đánh bắt của HTX là x (tấn) với x>0
Thời gian dự định đánh bắt: \(\dfrac{x}{20}\) tuần
Thực tế mỗi tuần HTX đánh bắt được: \(20+6=26\) tấn
Do vượt mức 10 tấn nên số cá thực tế đánh bắt được: \(x+10\) tấn
Thời gian thực tế HTX đánh bắt: \(\dfrac{x+10}{26}\)
Do HTX hoàn thành kế hoạch sớm 1 tuần nên ta có pt:
\(\dfrac{x}{20}-\dfrac{x+10}{26}=1\)
\(\Leftrightarrow\dfrac{3x}{260}=\dfrac{18}{13}\)
\(\Rightarrow x=120\) (tấn)
10 tháng 3 2022
\(\dfrac{7}{x-1}-\dfrac{1}{3\left(x+1\right)}=\dfrac{x}{x^2-1}\left(x\ne\pm1\right).\\ \Leftrightarrow\dfrac{21x+21-x+1}{x^2-1}=\dfrac{3x}{x^2-1}.\\ \Rightarrow17x=-22.\\ \Leftrightarrow x=\dfrac{-22}{17}\left(TM\right).\)
\(\dfrac{3x}{x-2}-\dfrac{x}{x-5}-\dfrac{2x}{x^2-7x+10}=0\left(x\ne2;5\right).\\ \Leftrightarrow\dfrac{3x}{x-2}-\dfrac{x}{x-5}-\dfrac{2x}{\left(x-5\right)\left(x-2\right)}=0.\\ \Rightarrow3x^2-15x-x^2+2x-2x=0.\\ \Leftrightarrow2x^2-15x=0.\\ \Leftrightarrow x\left(2x-15\right)=0.\Leftrightarrow\left[{}\begin{matrix}x=0.\\x=\dfrac{15}{2}.\end{matrix}\right.\)
(TMĐK).
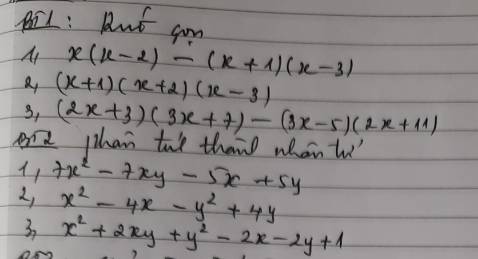
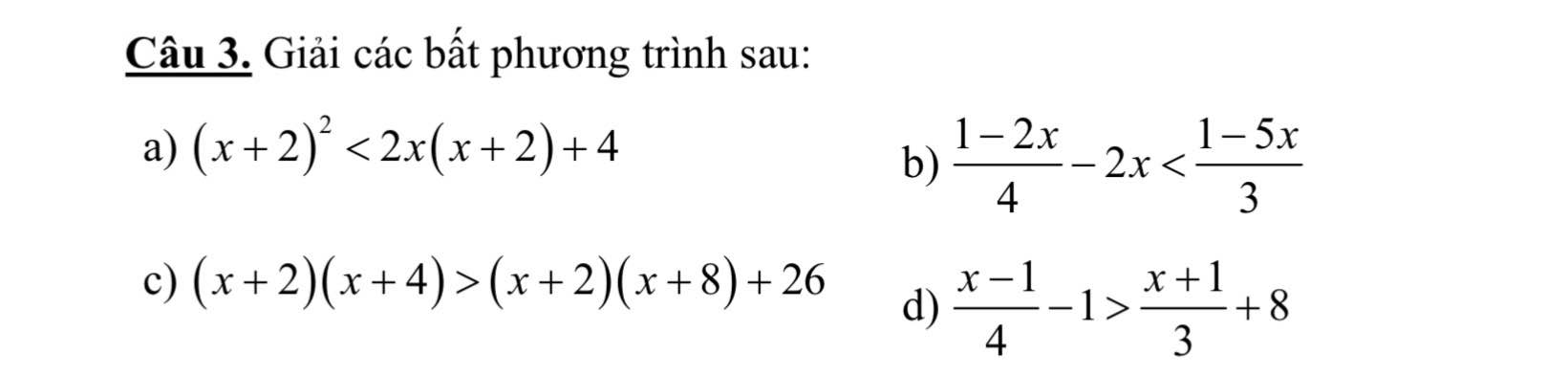
Chọn D