
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Câu 2:
\(B=\left(\dfrac{\sqrt{x}\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\right)\cdot\dfrac{x-1}{2x+2\sqrt{x}-\sqrt{x}-1}\)
\(=\left(\dfrac{\sqrt{x}+\sqrt{x}+3}{\left(\sqrt{x}-1\right)}\right)\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(2\sqrt{x}-1\right)}\)
\(=\dfrac{2\sqrt{x}+3}{2\sqrt{x}-1}\)
Để B<0 thì \(2\sqrt{x}-1< 0\)
=>\(2\sqrt{x}< 1\)
=>0<x<1/4


Bài 1 :
\(a,2\sqrt{50}-3\sqrt{72}+\sqrt{98}=2\sqrt{2.25}-3\sqrt{2.36}+\sqrt{2.49}=10\sqrt{2}-18\sqrt{2}+7\sqrt{2}\) = \(-\sqrt{2}\)
\(b,\sqrt{\left(3-\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}-\sqrt{7}\right)^2}+\sqrt{28}\) = \(\left|3-\sqrt{5}\right|-\left|\sqrt{5}-\sqrt{7}\right|+\sqrt{7.4}=3-\sqrt{5}-\sqrt{5}+\sqrt{7}+2\sqrt{7}=3-2\sqrt{5}+3\sqrt{7}\)
\(c,\sqrt{7-4\sqrt{3}}+\sqrt{7+4\sqrt{3}}=\sqrt{3-2.2\sqrt{3}+4}+\sqrt{3+2.2\sqrt{3}+4}=\)\(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{\left(\sqrt{3}+2\right)^2}=\left|-\left(2-\sqrt{3}\right)\right|+\left|\sqrt{3}+2\right|=2-\sqrt{3}+\sqrt{3}+2=4\)


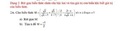



 câu 2 mn ơi mai mk phải hk r
câu 2 mn ơi mai mk phải hk r
 lm hộ mk vs
lm hộ mk vs







 Giúp mình với
Giúp mình với
Bạn kiểm tra lại điều kiện của đề bài nhé vì x ở dưới mẫu ko thể = 0 được
a) M = \(\left(\frac{\sqrt{x}}{\sqrt{x}-1}+\frac{\sqrt{x}}{x-1}\right)\): \(\left(\frac{2}{x}-\frac{2-x}{x\sqrt{x}+x}\right)\) ( ĐKXĐ : x > 0 , x\(\ne\)1)
M = \(\frac{\sqrt{x}\left(\sqrt{x}+1\right)+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\):\(\frac{2\left(\sqrt{x}+1\right)-2+x}{x\left(\sqrt{x}+1\right)}\)
M = \(\frac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\):\(\frac{x+2\sqrt{x}}{x\left(\sqrt{x}+1\right)}\)
M = \(\frac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(\sqrt{x-1}\right)\left(\sqrt{x}+1\right)}.\frac{x\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+2\right)}\)
M = \(\frac{x}{\sqrt{x}-1}\)
b) M = \(\frac{x}{\sqrt{x}-1}\)( ĐKXĐ : x > 0, x\(\ne\)1)
Ta có : \(\frac{x}{\sqrt{x}-1}\)= \(\frac{-1}{2}\)
\(\Rightarrow\)2x = -1 ( \(\sqrt{x}-1\))
\(\Leftrightarrow\) 2x + \(\sqrt{x}\)-1 = 0
\(\Leftrightarrow\) \(\left(2\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\)= 0
\(\Leftrightarrow\)\(\orbr{\begin{cases}\sqrt{x}=\frac{1}{2}\\\sqrt{x}=-1\end{cases}\Rightarrow}x=\frac{1}{4}\left(TM\text{Đ}K\right)\)
Vậy x =\(\frac{1}{4}\) để M = \(\frac{-1}{2}\)