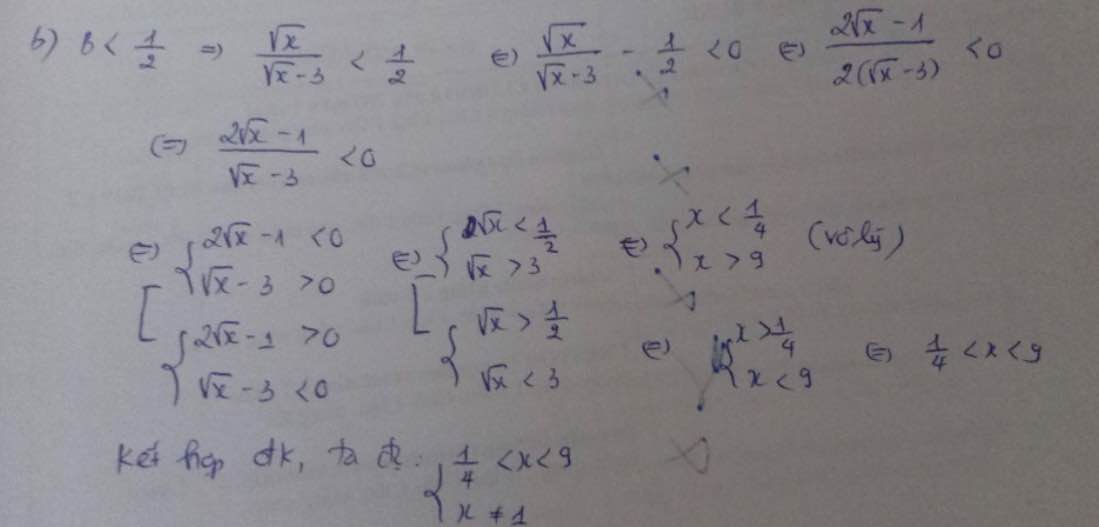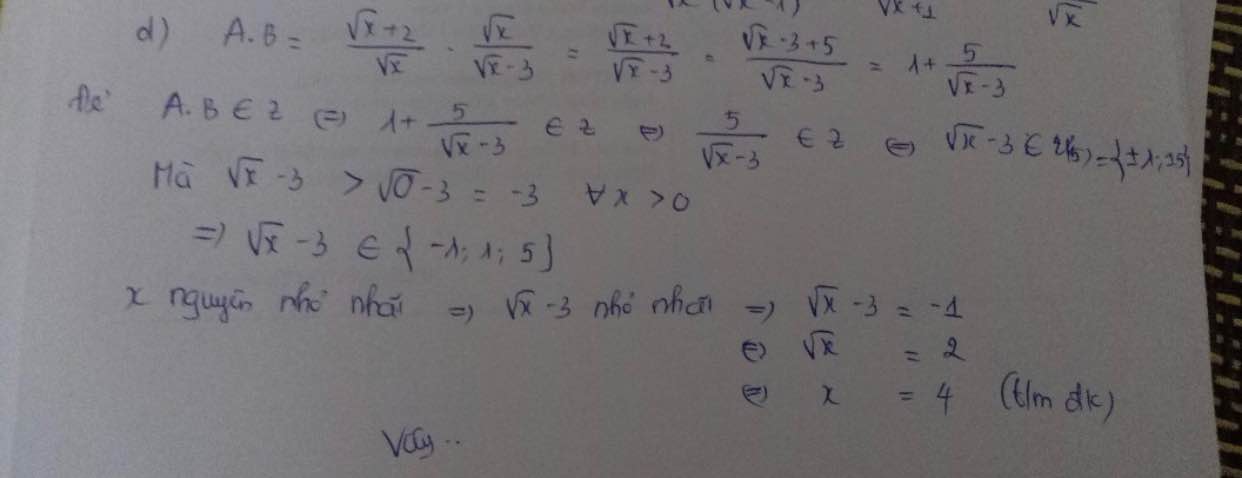Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a) x\(^3\)+3x\(^2\)-2x-6=0
⇔(x+3)(x+\(\sqrt{2}\))(x-\(\sqrt{2}\))
⇔x+3=0 hoặc x+\(\sqrt{2}\)=0 hoặc x-\(\sqrt{2}\)=0
⇔x=-3 hoặc x=-\(\sqrt{2}\) hoặc x=\(\sqrt{2}\)
b)2x\(^3\)+7x\(^2\)+7x+2=0
⇔(x+1)(2x+1)(x+2)=0
⇔x+1=0 hoặc2x+1=0 hoặc x+2=0
⇔x=-1 hoặcx=-\(\dfrac{1}{2}\) hoặc x=-2
c)x\(^3\)+7x\(^2\)-56x+48=0
⇔(x-1)(x-4)(x+12)=0
⇔x-1=0 hoặcx-4=0 hoặcx+12=0
⇔x =1hoặcx=4 hoặcx=-12

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB, ta được:
\(AM\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC, ta được:
\(AN\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

Bào 7:
Áp dụng hệ thức lượng trong tam giác vuông có:
\(cos\widehat{BAH}=\dfrac{AH}{AB}=\dfrac{3}{7}\)\(\Rightarrow AH=\dfrac{3AB}{7}\)
\(AB^2+AC^2=BC^2=196\) \(\Leftrightarrow AB^2=196-AC^2\)
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
\(\Leftrightarrow\dfrac{1}{196-AC^2}+\dfrac{1}{AC^2}=\dfrac{1}{\dfrac{9}{49}AB^2}\)
\(\Leftrightarrow\dfrac{1}{196-AC^2}+\dfrac{1}{AC^2}=\dfrac{49}{9\left(196-AC^2\right)}\)
\(\Leftrightarrow\dfrac{9AC^2}{9AC^2\left(196-AC^2\right)}+\dfrac{9\left(196-AC^2\right)}{9AC^2\left(196-AC^2\right)}=\dfrac{49AC^2}{9AC^2\left(196-AC^2\right)}\)
\(\Rightarrow9AC^2+9\left(196-AC^2\right)=49AC^2\)
\(\Leftrightarrow AC^2=36\) =>AC=6
Vậy AC=6 cm

\(11,\\ a,M=\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\\ b,M=\dfrac{\sqrt{a}-1}{\sqrt{a}}=1-\dfrac{1}{\sqrt{a}}< 1\left(\dfrac{1}{\sqrt{a}}>0\right)\)
\(9,\\ a,=\left|2-\sqrt{7}\right|=\sqrt{7}-2\\ b,=5\sqrt{3}+4\sqrt{3}-10\sqrt{3}=-\sqrt{3}\\ c,=3-4+2=1\\ d,=6\sqrt{3a}-4\sqrt{3a}=2\sqrt{3a}\\ 10,\)
a, Áp dụng HTL: \(x=\sqrt{9\cdot25}=15\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}8^2=10x\\y^2=x\left(x+10\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=6,4\\y=\sqrt{6,4\cdot16,4}\approx10,245\end{matrix}\right.\)

36B
37C
38D
39B
40D
41A
42B
43B
44A
45B
46B
47A
48C
50B
51B
52B
53D
54C
55D
56C
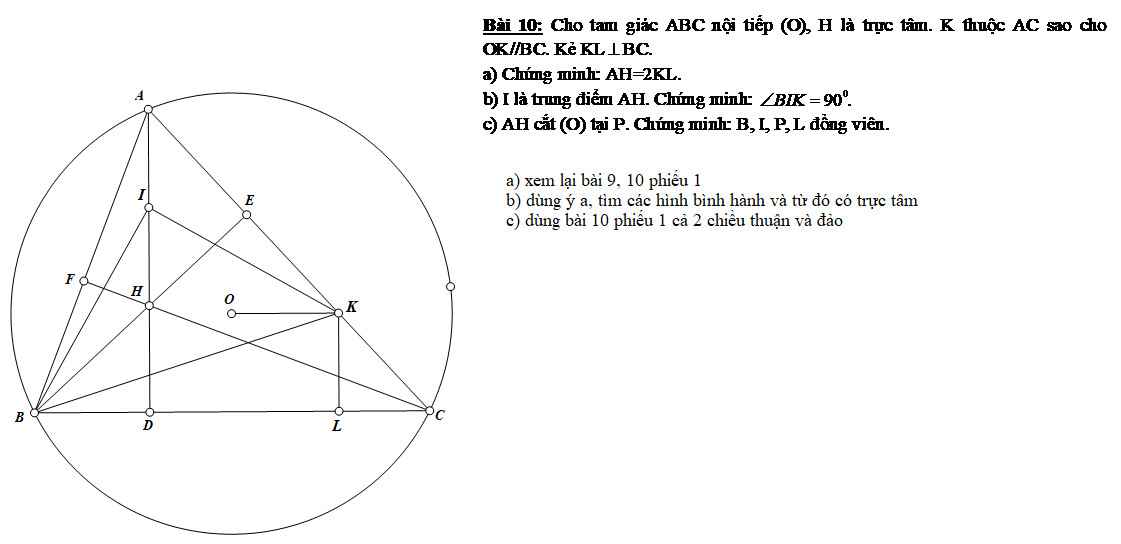




 Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp
Em cần giúp câu c và d ạ, mn giúp em với em đang cần gấp