
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(P=\dfrac{a\sqrt{a}-1}{a-\sqrt{a}}-\dfrac{a\sqrt{a}+1}{a+\sqrt{a}}+\left(\sqrt{a}-\dfrac{1}{\sqrt{a}}\right)\left(\dfrac{3\sqrt{a}}{\sqrt{a}-1}-\dfrac{\sqrt{a}+2}{\sqrt{a}+1}\right)\)
\(=\dfrac{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+1\right)\left(a-\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}+1\right)}+\dfrac{a-1}{\sqrt{a}}\cdot\dfrac{3\sqrt{a}\left(\sqrt{a}+1\right)-\left(\sqrt{a}+2\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{a+\sqrt{a}+1-a+\sqrt{a}-1}{\sqrt{a}}+\dfrac{3a+3\sqrt{a}-\left(a-\sqrt{a}+2\sqrt{a}-2\right)}{\sqrt{a}}\)
\(=2+\dfrac{3a+3\sqrt{a}-a+\sqrt{a}-2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\sqrt{a}+2a+2\sqrt{a}+2}{\sqrt{a}}\)
\(=\dfrac{2\left(a+2\sqrt{a}+1\right)}{\sqrt{a}}\)
\(=\dfrac{2\left(\sqrt{a}+1\right)^2}{\sqrt{a}}\)
b) Ta có: \(P-6=\dfrac{2\left(\sqrt{a}+1\right)^2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2a+4\sqrt{a}+2-6\sqrt{a}}{\sqrt{a}}\)
\(=\dfrac{2\left(a-\sqrt{a}+1\right)}{\sqrt{a}}>0\forall a\) thỏa mãn ĐKXĐ
hay P>6

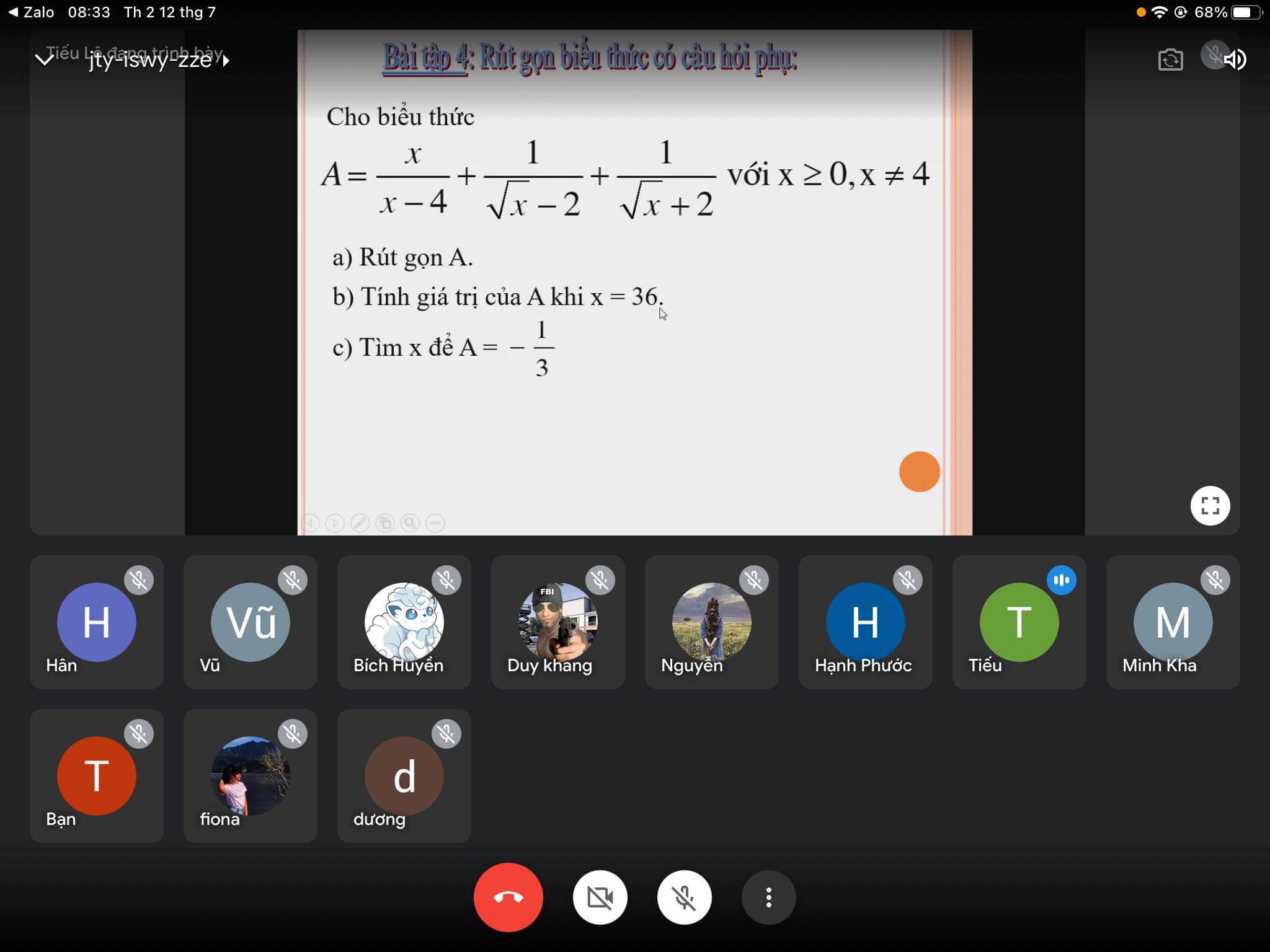
a) Ta có: \(A=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
b) Thay x=36 vào A, ta được:
\(A=\dfrac{6}{6-2}=\dfrac{6}{4}=\dfrac{3}{2}\)
c) Để \(A=\dfrac{-1}{3}\) thì \(\dfrac{\sqrt{x}}{\sqrt{x}-2}=\dfrac{-1}{3}\)
\(\Leftrightarrow3\sqrt{x}=-1\left(\sqrt{x}-2\right)\)
\(\Leftrightarrow3\sqrt{x}+\sqrt{x}=2\)
\(\Leftrightarrow\sqrt{x}=\dfrac{1}{2}\)
hay \(x=\dfrac{1}{4}\)

a, Ta có : \(AC^2=AB^2+BC^2=40^2+42^2=3364\Rightarrow AC=58\)cm * đúng *
Vậy tam giác ABC vuông tại B
b, \(\sin A=\dfrac{BC}{AC}=\dfrac{42}{58}=\dfrac{21}{29}\)
\(\cos A=\dfrac{AB}{AC}=\dfrac{40}{58}=\dfrac{20}{29}\)
\(\tan A=\dfrac{BC}{AB}=\dfrac{42}{40}=\dfrac{21}{20}\)
\(\cot aA=\dfrac{AB}{BC}=\dfrac{40}{42}=\dfrac{20}{21}\)

\(a,\sqrt{-5x-10}\) có nghĩa \(\Leftrightarrow-5x-10\ge0\Leftrightarrow-5x\ge10\Leftrightarrow x\le-2\)
\(b,\sqrt{\dfrac{-2}{3x-1}}\) có nghĩa \(\Leftrightarrow\dfrac{-2}{3x-1}\ge0\Leftrightarrow3x-1< 0\Leftrightarrow x< \dfrac{1}{3}\)
\(c,\sqrt{\dfrac{2x-3}{2x^2+1}}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}2x-3\ge0\\2x^2+1>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ge3\\2x^2>-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x^2>-\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow x\ge\dfrac{3}{2}\)
\(d,\sqrt{\dfrac{3x-2}{x^2-2x+4}}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}3x-2\ge0\\x^2-2x+4>0\end{matrix}\right.\)
\(\Leftrightarrow3x\ge2\)
\(\Leftrightarrow x\ge\dfrac{2}{3}\)
\(e,\sqrt{x^2-8x-9}\) có nghĩa \(\Leftrightarrow x^2-8x-9\ge0\)
\(\Leftrightarrow x^2+x-9x-9\ge0\)
\(\Leftrightarrow x\left(x+1\right)-9\left(x+1\right)\ge0\)
\(\Leftrightarrow\left(x-9\right)\left(x+1\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-9\ge0\\x+1\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-9\le0\\x+1\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge9\\x\ge-1\end{matrix}\right.\\\left\{{}\begin{matrix}x\le9\\x\le-1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge9\\x\le-1\end{matrix}\right.\)
\(f,\sqrt{\dfrac{2x-4}{5-x}}\) có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}2x-4\ge0\\5-x>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge2\\x< 5\end{matrix}\right.\)
a: ĐKXĐ: -5x-10>=0
=>x<=-2
b: ĐKXĐ: 3x-1<0
=>x<1/3
c: ĐKXĐ: 2x-3>=0
=>x>=3/2
e: ĐKXĐ: (x-9)(x+1)>=0
=>x>=9 hoặc x<=-1
d: ĐKXĐ: 3x-2>=0
=>x>=2/3

\(9,=\dfrac{\sqrt{5}+1-\sqrt{5}+1}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}=\dfrac{2}{4}=\dfrac{1}{2}\\ 10,=\dfrac{\sqrt{5}+2+\sqrt{5}-2}{\left(\sqrt{5}-2\right)\left(\sqrt{5}+2\right)}=2\sqrt{5}\\ 11,=\dfrac{8+6\sqrt{2}-8+6\sqrt{2}}{\left(4-3\sqrt{2}\right)\left(4+3\sqrt{2}\right)}=\dfrac{12\sqrt{2}}{-2}=-6\sqrt{2}\\ 12,=\dfrac{2+\sqrt{6}+2-\sqrt{6}}{\left(2-\sqrt{6}\right)\left(2+\sqrt{6}\right)}=\dfrac{4}{-2}=-2\\ 13,=\sqrt{2}-1+\sqrt{2}+3=2\sqrt{2}+2\\ 14,=2-\sqrt{3}+\sqrt{3}-1=1\\ 15,=3-\sqrt{5}+\sqrt{5}-2=1\)

a) Ta có: \(S=\left(1+\dfrac{\sqrt{x}}{x+1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{x\sqrt{x}+\sqrt{x}-x-1}\right)\)
\(=\dfrac{x+\sqrt{x}+1}{x+1}:\dfrac{1-x-1}{\left(\sqrt{x}-1\right)\left(x+1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{-x}\cdot\dfrac{\left(\sqrt{x}-1\right)}{ }\)
\(=\dfrac{1-x\sqrt{x}}{x}\)
b) Thay \(x=4-2\sqrt{3}\) vào S, ta được:
\(S=\dfrac{1-\left(4-2\sqrt{3}\right)\left(\sqrt{3}-1\right)}{4-2\sqrt{3}}\)
\(=\dfrac{1-\left(4\sqrt{3}-4-6+2\sqrt{3}\right)}{4-2\sqrt{3}}\)
\(=\dfrac{1-2\sqrt{3}+10}{4-2\sqrt{3}}=\dfrac{9-2\sqrt{3}}{4-2\sqrt{3}}\)
\(=\dfrac{\left(9-2\sqrt{3}\right)\left(4+2\sqrt{3}\right)}{4}\)
\(=\dfrac{36+18\sqrt{3}-8\sqrt{3}-12}{4}\)
\(=\dfrac{24+10\sqrt{3}}{4}=\dfrac{12+5\sqrt{3}}{2}\)
a)\(S=\left(\dfrac{x+1+\sqrt{x}}{x+1}\right):\left(\dfrac{x+1-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+1\right)}\right)\) \(đk:x\ne\pm1\)
\(S=\dfrac{x+1+\sqrt{x}}{x+1}.\dfrac{\left(\sqrt{x}-1\right)\left(x+1\right)}{\left(\sqrt{x}-1\right)^2}\)
\(S=\dfrac{x+1+\sqrt{x}}{\sqrt{x}-1}\)
b)\(x=4-2\sqrt{3}=\left(\sqrt{3}-1\right)^2\left(TMĐK\right)\)
\(\sqrt{x}=\sqrt{3}-1\)
Từ đó ta có :
\(S=\dfrac{4-2\sqrt{3}+1+\sqrt{3}-1}{\sqrt{3}-1-1}\)
\(S=-5-2\sqrt{3}\)

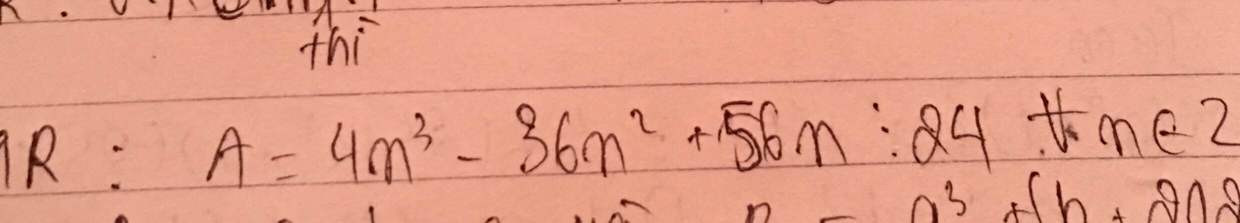

 giúp mik vs ạ. Cảm ơn mn
giúp mik vs ạ. Cảm ơn mn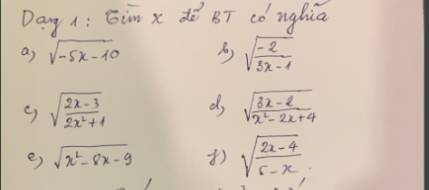
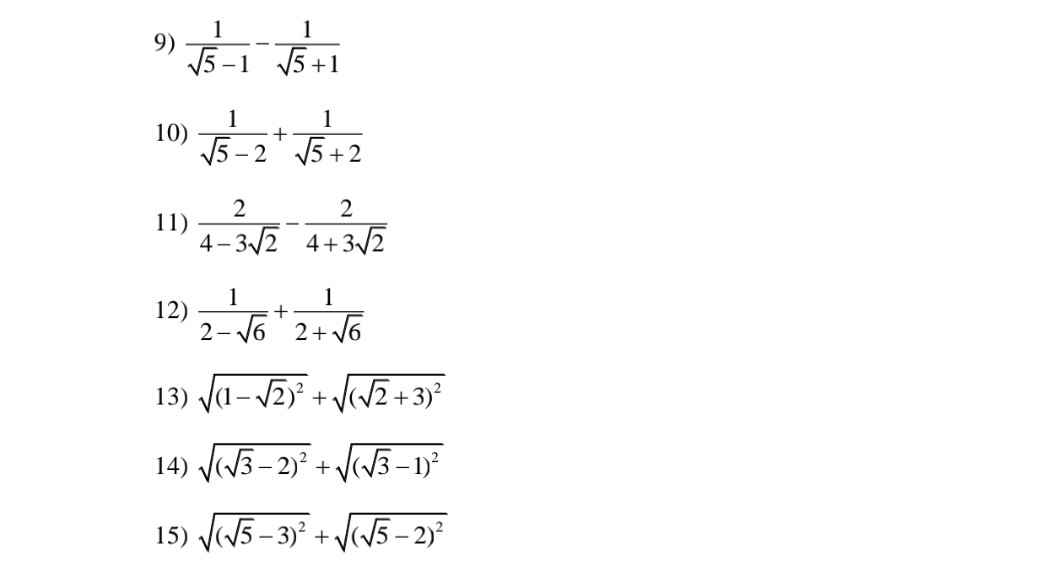



Lời giải:
$A=4n^3-36n^2+56n=4n(n^2-9n+14)=4n(n-2)(n-7)$
Vì $n-2,n-7$ khác tính chẵn lẻ nên 1 trong 2 số sẽ là số chẵn.
$\Rightarrow n(n-2)(n-7)\vdots 2$
$\Rightarrow =4n(n-2)(n-7)\vdots 8(*)$
Lại có:
Nếu $n$ chia hết cho $3$ thì $A=4n(n-2)(n-7)\vdots 3$
Nếu $n$ chia $3$ dư $1$ thì $n-7\vdots 3\Rightarrow A\vdots 3$
Nếu $n$ chia $3$ dư $2$ thì $n-2\vdots 3\Rightarrow A\vdots 3$
Tóm lại $A\vdots 3(**)$
Từ $(*); (**)$ mà $(3,8)=1$ nên $A\vdots 24$.
Ta có đpcm.